题目内容
19.为使“居者有其屋”,某市加快了廉租房的建设力度.2014年市政府共投资2亿元人民币建设了廉租房10万平方米,预计到2016年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2016年底共建设了多少万平方来廉租房.
分析 (1)设每年市政府投资的增长率为x.根据到2016年底三年共累计投资9.5亿元人民币建设廉租房,列方程求解;
(2)先求出单位面积所需钱数,再用累计投资÷单位面积所需钱数可得结果.
解答 解:(1)设每年市政府投资的增长率为x,
根据题意,得:2+2(1+x)+2(1+x)2=9.5,
解得:x=-3.5(舍去)或x=0.5=50%.
答:每年市政府投资的增长率为50%;
(2)到2016年底共建廉租房面积=9.5÷$\frac{2}{10}$=47.5(万平方米)
答:到2016年底共建设了47.5万平方来廉租房.
点评 主要考查了一元二次方程的实际应用,解题的关键是掌握增长率问题中的一般公式为a(1+x)n,其中n为共增长了几年,a为第一年的原始数据,x是增长率.

练习册系列答案
相关题目
10.大于-4的负整数个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 无数个 |
4.下列说法:
①在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC为直角三角形;
②已知直角三角形的面积为2,两直角边的比为1:2,则斜边长的平方为10;
③在Rt△ABC中,若两边长分别为3和4,则第三边长为5;
④已知等腰三角形的面积为12,底边上的高为4,则腰长为5.
其中正确结论的序号是( )
①在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC为直角三角形;
②已知直角三角形的面积为2,两直角边的比为1:2,则斜边长的平方为10;
③在Rt△ABC中,若两边长分别为3和4,则第三边长为5;
④已知等腰三角形的面积为12,底边上的高为4,则腰长为5.
其中正确结论的序号是( )
| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ②④ |
8.设y=ax2+bx+1(a≠0),y的最大值为1,则( )
| A. | b<0 | B. | b=0 | C. | 0<b<1 | D. | b≥1 |
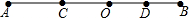 (1)如图,线段AB=4,点O是线段AB上一点,C,D分别是线段OA,OB的中点,则线段CD的长为多少?
(1)如图,线段AB=4,点O是线段AB上一点,C,D分别是线段OA,OB的中点,则线段CD的长为多少?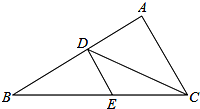 如图所示,在△ABC中,CD平分∠ACB,DE∥AC.
如图所示,在△ABC中,CD平分∠ACB,DE∥AC.