题目内容
8.设y=ax2+bx+1(a≠0),y的最大值为1,则( )| A. | b<0 | B. | b=0 | C. | 0<b<1 | D. | b≥1 |
分析 当x=0时,y=1,故此方程的对称轴为x=0,从而可确定出b的值.
解答 解:将x=0代入得:y=1,
∵y的最大值为1,
∴函数的对称轴为x=0,即$-\frac{b}{2a}=0$.
解得:b=0.
故选:B.
点评 本题主要考查的是二次函数的最值,根据函数的最值得到抛物线的对称轴为x=0是解题的关键.

练习册系列答案
相关题目
16.已知$\root{3}{(x-2)^{3}}$+$\sqrt{(x-2)^{2}}$=0,则x的取值范围为( )
| A. | x≤2 | B. | x<2 | C. | x≥2 | D. | x>2 |
13.直角三角形的斜边长为8,内切圆的半径为1,则这个三角形的周长为( )
| A. | 21 | B. | 20 | C. | 19 | D. | 18 |
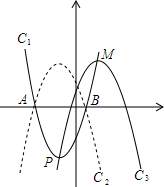 如图,已知抛物线C1:y=a(x+2)2-5的顶点为P1与x轴相交于A、B两点(点A在点B的左侧),且点B的坐标为(1,0);
如图,已知抛物线C1:y=a(x+2)2-5的顶点为P1与x轴相交于A、B两点(点A在点B的左侧),且点B的坐标为(1,0);