题目内容

2．已知CD是Rt△ABC斜边上的高，且CD=3cm．AD，BD是方程x2-6x+4=0的两根，求△ABC的面积．

分析 根据根与系数的关系得到AD+BD=6，然后又三角形的面积公式即可得到结论．

解答 解：∵AD、BD是方程x2-6x+4=0的两根，
∴AD+BD=6，
∴S△ABC=$\frac{1}{2}$（AD+BD）•CD=$\frac{1}{2}×6×3$=9．

点评 本题考查了一元二次方程根与系数的关系，三角形的面积，解题关键是得到所求三角形相应的底的长．

练习册系列答案
相关题目
19．为使“居者有其屋”，某市加快了廉租房的建设力度．2014年市政府共投资2亿元人民币建设了廉租房10万平方米，预计到2016年底三年共累计投资9.5亿元人民币建设廉租房，若在这两年内每年投资的增长率相同．
（1）求每年市政府投资的增长率；
（2）若这两年内的建设成本不变，求到2016年底共建设了多少万平方来廉租房．
20．某城市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨1.9元收费．如果超过20吨，未超过的部分按每吨1.9元收费，超过的部分按每吨2.8元收费．设某户每月用水量为x吨，应收水费为y．
（1）某户3月份用水10吨，则该户居民应交19元．若该户居民8月用水30吨，则该户居民应交66元；
（2）分别写出每月用水量未超过20吨和超过20吨，水费y元与用水量x之间的函数关系式；
（3）若某户居民4月份的水费为52元，问该户居民4月份实际用水多少吨？
（4）若某户居民5月份水费平均为每吨2.2元，求该户5月份用水多少吨？
10．在图1至图5中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE=2b，且边AD和AE在同一直线上．

操作示例：
当2b＜a时，如图（1），在BA上选取点G，使BG=b，连接FG和CG，裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH．
思考发现：
小明在操作后发现：该剪拼方法就是先将△FAG绕点F逆时针旋转90度到△FEH的位置，易知EH与AD在同一直线上．连接CH，由剪拼方法可得DH=BG，故△CHD≌△CGB，从而又可将△CGB绕点G顺时针旋转90度到△CHD的位置．这样，对于剪拼得到的四边形FGCH（如图），过点F作FM⊥AE于点M（图略），利用SAS公理可判断△HFM≌△CHD，易得FH=HC=GC=FG，．∠FHC=90°进而根据正方形的判定方法，可以判断出四边形FGCH是正方形．
实践探究：
正方形的面积是b2+a2；（用含a，b，的式子表示）
类比图1的剪拼方法，请你就图2-图4的三种情形分别画出剪拼成一个新正方形的示意图．
联想拓展：
小明通过探究后发现：当b≤a，此类图形都能剪拼成正方形，且所选取的点G的位置在BA方向上随着b的增大不断上移；当b＞a时，如图的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．
17．下列说法不正确的是（　　）
A．球的截面一定是圆
B．组成长方体的各个面中不可能有正方形
C．从三个不同的方向看正方体，得到的都是正方形
D．圆锥的截面可能是圆
7．（1）-7的相反数是7，它的绝对值是7；
（2）-2$\frac{2}{5}$的倒数是$-\frac{5}{12}$
（3）倒数等于它本身的有理数是±1．
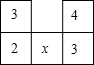14．如图所示是由几个相同的小正方体所组成的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数，请画出这个几何体从正面看和从左面看到的图形，其中x是平方等于本身的正整数．
11．分式$\frac{x}{4a}$，$\frac{x-y}{{x}^{2}-{y}^{2}}$，$\frac{a+b}{a-b}$，$\frac{（x+y）^{2}}{xy+{y}^{2}}$，$\frac{4}{2x-6}$中，最简分式的个数是（　　）
A．1个B．2个C．3个D．4个
12．当x=$\frac{1}{2}$，y=-2时，代数式$\frac{4x-2y}{xy}$的值是-6．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网