题目内容
14.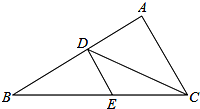 如图所示,在△ABC中,CD平分∠ACB,DE∥AC.
如图所示,在△ABC中,CD平分∠ACB,DE∥AC.(1)图中哪个三角形是等腰三角形?请说明理由.
(2)若∠A=80°,∠B=40°,求∠DEC的度数.
分析 (1)由角平分线的定义、平行线的性质以及等量代换证得∠1=∠3,根据“等角对等边”推知ED=EC,即△DEC是等腰三角形;
(2)利用三角形内角和定理知∠ACB=60°,然后由“两直线平行,同旁内角互补”来求∠DEC的度数.
解答  解:(1)△DEC是等腰三角形.理由如下:
解:(1)△DEC是等腰三角形.理由如下:
如图,∵CD平分∠ACB,
∴∠1=∠2.
又∵DE∥AC,
∴∠2=∠3,
∴∠1=∠3,
∴ED=EC,即△DEC是等腰三角形;
(2)∵在△ABC中,∠A=80°,∠B=40°,
∴∠ACB=180°-∠A=∠B=60°,
∵DE∥AC,
∴∠DEC=180°-∠ACB=120°,即∠DEC的度数是120°.
点评 本题考查了平行线的性质、等腰三角形的判定与性质,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
17.下列说法不正确的是( )
| A. | 球的截面一定是圆 | |
| B. | 组成长方体的各个面中不可能有正方形 | |
| C. | 从三个不同的方向看正方体,得到的都是正方形 | |
| D. | 圆锥的截面可能是圆 |
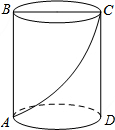 如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.
如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.