题目内容
点A(x1,y1),B(x2,y2),C(x3,y3)分别是y=-
图象上三点,且x1>x2>0>x3,则下列结论正确的是( )
| 1 |
| x |
| A、y1>y2>y3 |
| B、y1>y3>y2 |
| C、y3>y1>y2 |
| D、y1>y2>y3 |
考点:反比例函数图象上点的坐标特征
专题:
分析:先根据反比例函数的解析式判断出函数图象所在的象限及的增减性,再根据x1>x2>0>x3,判断出各点所在的象限,进而可得出结论.
解答:解:∵反比例函数y=-
中,k=-1<0,
∴此函数图象的两个分支分别位于二四象限,在每一象限内y随x的增大而增大.
∵x1>x2>0>x3,
∴A(x1,y1),B(x2,y2)位于第四象限,C(x3,y3)位于第二象限,
∴y2<y1<0<y3.
故选C.
| 1 |
| x |
∴此函数图象的两个分支分别位于二四象限,在每一象限内y随x的增大而增大.
∵x1>x2>0>x3,
∴A(x1,y1),B(x2,y2)位于第四象限,C(x3,y3)位于第二象限,
∴y2<y1<0<y3.
故选C.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
下列判断中正确的是( )
| A、6a2bc与bca2不是同类项 | ||
B、
| ||
| C、25xyz是三次单项式 | ||
| D、3x2-y+5xy2是二次三项式 |
已知△ABC与△DEF全等,∠A=∠D=70°,∠B=60°,则∠F的度数是( )
| A、50° |
| B、60° |
| C、60°或50° |
| D、70°或50° |
由方程组
可得出关于x于y之间的关系式为( )
|
| A、2x-y=-4 |
| B、2x-y=4 |
| C、2x+y=-4 |
| D、2x+y=4 |
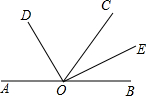 如图,A、O、B三点在同一直线上,OC是任一条射线,OD、OE分别是∠AOC和∠BOC的平分线.
如图,A、O、B三点在同一直线上,OC是任一条射线,OD、OE分别是∠AOC和∠BOC的平分线. 已知,如图,∠C=90°,∠B=30°,AD是△ABC的角平分线,求证:BD=2CD.
已知,如图,∠C=90°,∠B=30°,AD是△ABC的角平分线,求证:BD=2CD.