题目内容
 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
(1)若点A的纵坐标为6,点B的横坐标为3,AC=2CM,求反比例函数的解析式;
(2)求证:AB∥MN.
考点:反比例函数综合题
专题:
分析:(1)根据已知求得CM=2,进而求得B的坐标,代入y=
(x>O,k是常数)即可求得k的值,从而求得反比例函数的解析式;
(2)把A点纵坐标代入(1)求得的解析式即可求得A的坐标,根据A、B两点坐标可得AC=4,BC=2,ON=2,OM=1,则
=
=
,再由∠ACB=∠NOM=90°,可得△ACB∽△NOM,得出∠OMN=∠ABC,进而求得∠MNC=∠ABC,即可证得结论.
| k |
| x |
(2)把A点纵坐标代入(1)求得的解析式即可求得A的坐标,根据A、B两点坐标可得AC=4,BC=2,ON=2,OM=1,则
| ON |
| OM |
| AC |
| BC |
| 1 |
| 2 |
解答:解:(1)∵点A的纵坐标为6,AC=2CM,AM⊥X轴,
∴CM=2,
∵BN⊥y轴,
∴BN∥x轴,
∴B(3,2),
∵反比例函数y=
(x>O,k是常数)的图象经过点B,
∴k=6,
∴反比例函数解析式为y=
;
(2)∵点A的纵坐标为6,且反比例函数y=
的图象经过点A,
∴x=1,
∴A(1,6),
∴BC=3-1=2,AC=6-2=4,
∵
=
=
,∠MON=∠ACB=90°,
∴△ACB∽△NOM;
∴∠OMN=∠ABC,
∵BN⊥y轴,∠MON=90°,
∴BN∥OM,
∴∠OMN=∠MNC,
∴∠MNC=∠ABC,
∴AB∥MN.
∴CM=2,
∵BN⊥y轴,
∴BN∥x轴,
∴B(3,2),
∵反比例函数y=
| k |
| x |
∴k=6,
∴反比例函数解析式为y=
| 6 |
| x |
(2)∵点A的纵坐标为6,且反比例函数y=
| 6 |
| x |
∴x=1,
∴A(1,6),
∴BC=3-1=2,AC=6-2=4,
∵
| ON |
| OM |
| AC |
| BC |
| 1 |
| 2 |
∴△ACB∽△NOM;
∴∠OMN=∠ABC,
∵BN⊥y轴,∠MON=90°,
∴BN∥OM,
∴∠OMN=∠MNC,
∴∠MNC=∠ABC,
∴AB∥MN.
点评:此题反比例函数的综合应用,考查了待定系数法求解析式,三角形相似的判定和性质,平行线的判定和性质等,关键是掌握凡是函数图象经过的点,必然能使函数解析式左右相等.

练习册系列答案
相关题目
由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是( )


| A、3 | B、4 | C、5 | D、6 |
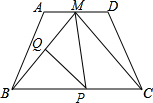 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,BC=8,MB=5
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,BC=8,MB=5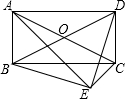 已知:如图,在四边形ABCD中,以AC为斜边作Rt△ACE,且∠BED为直角.求证:四边形ABCD是矩形.
已知:如图,在四边形ABCD中,以AC为斜边作Rt△ACE,且∠BED为直角.求证:四边形ABCD是矩形. 如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=DE=EC.求证:
如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=DE=EC.求证: 明月兔业养殖厂在兔舍外面开辟一个面积为20平方米的长方形活动场地,准备一边靠墙,其余三边利用长14米的旧围栏,已知兔舍墙面宽6米,问围成长方形的长和宽各是多少米?
明月兔业养殖厂在兔舍外面开辟一个面积为20平方米的长方形活动场地,准备一边靠墙,其余三边利用长14米的旧围栏,已知兔舍墙面宽6米,问围成长方形的长和宽各是多少米?