题目内容
17.一个平行四边形的周长为70cm,两边的差是5cm,则平行四边形较长边长20cm.分析 设该平行四边形的两边长分别为xcm、ycm,根据平行四边形性质可得2(x+y)=70,由两边的差是5cm可得x-y=5,解方程组可得.
解答 解:设该平行四边形的两边长分别为xcm,ycm,根据题意,
得:$\left\{\begin{array}{l}{2(x+y)=70}\\{x-y=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=15}\end{array}\right.$,
则平行四边形较长边长为20cm,较短边长为15cm,
故答案为:20.
点评 本题主要考查平行四边形的性质及二元一次方程组的应用,根据平行四边形对边相等及题意列出方程组是关键,解方程组是基本.

练习册系列答案
相关题目
11.计算:$\frac{\sqrt{3}+2\sqrt{5}+\sqrt{7}}{(\sqrt{3}+\sqrt{5})(\sqrt{5}+\sqrt{7})}$=( )
| A. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | B. | $\frac{\sqrt{7}-\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}-\sqrt{7}}{2}$ | D. | $\frac{-\sqrt{7}-\sqrt{3}}{2}$ |
2.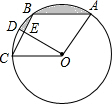 如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
 如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 4π-12$\sqrt{3}$ | B. | 4π-6$\sqrt{3}$ | C. | 4π | D. | 6π |
6.现有一只蜗牛和一只乌龟从同一点分别沿正东和正南方向爬行,蜗牛的速度为14厘米/分钟,乌龟的速度为48厘米/分钟,5分钟后,蜗牛和乌龟的直线距离为( )
| A. | 300厘米 | B. | 250厘米 | C. | 200厘米 | D. | 150厘米 |
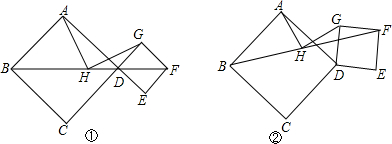
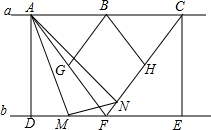 如图,直线a∥b,点A,B,C在直线a上,B是的AC中点,AC=4,分别过点A,C作直线b的垂线,垂足为D,E,F是直线b上的一个动点,连接AF,CF,若AF=CF.
如图,直线a∥b,点A,B,C在直线a上,B是的AC中点,AC=4,分别过点A,C作直线b的垂线,垂足为D,E,F是直线b上的一个动点,连接AF,CF,若AF=CF. 如图所示的一块地,∠ADC=90°,AD=3m,CD=4m,AB=13m,BC=12m,则这块地的面积是36m2.
如图所示的一块地,∠ADC=90°,AD=3m,CD=4m,AB=13m,BC=12m,则这块地的面积是36m2.