题目内容
14.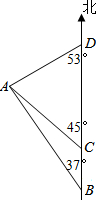 如图,一艘货船从港口B出发,沿正北方向航行至港口D,在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处时,测得A处在C处的西北方向上,航行至D处时,测得A处在C处的南偏西53°方向上,已知A,B之间的距离是100海里,
如图,一艘货船从港口B出发,沿正北方向航行至港口D,在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处时,测得A处在C处的西北方向上,航行至D处时,测得A处在C处的南偏西53°方向上,已知A,B之间的距离是100海里,(1)求货船与灯塔之间的最短距离及B,C之间的距离.
(2)若有一巡逻艇与货船从港口B同时出发,巡逻艇先直线航行到A处,在A处停留10分钟后,再以相同的速度直线航行至港口D,结果巡逻艇与货船同时到达港口D已知巡逻艇比货船每小时多航行25海里.求货船的速度.(参考数据:$sin37°≈\frac{3}{5},tan37°≈\frac{3}{4}$)
分析 (1)过点A作AO⊥BD,垂足为O.先解Rt△ABO,求出AO=AB•sin37°≈100×$\frac{3}{5}$=60,BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=80.再解Rt△ACO,得到CO=AO=60,那么BC=BO-CO=80-60=20海里;
(2)先解Rt△AOD,求出OD=OA•tan∠OAD≈60×$\frac{3}{4}$=45,AD=$\sqrt{O{A}^{2}+A{D}^{2}}$=75,那么BD=BO+OD=80+45=125.再证明△ABD是直角三角形,利用勾股定理求出AB=$\sqrt{B{D}^{2}-A{D}^{2}}$=100.设货船的速度为每小时x海里,则巡逻艇的速度为每小时(x+25)海里,等量关系为:巡逻艇行驶(AB+AD)所用的时间+$\frac{10}{60}$小时=货船行驶BD所用的时间,依此列出方程求解即可.
解答 解:(1)过点A作AO⊥BD,垂足为O.
在Rt△ABO中,∵AB=100海里,∠ABO=37°,
∴AO=AB•sin37°≈100×$\frac{3}{5}$=60,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=80.
在Rt△ACO中,∵AO=60,∠ACO=45°,
∴CO=AO=60,
∴BC=BO-CO=80-60=20,
答:货船与灯塔之间的最短距离约为60海里,B、C之间的距离约为20海里; (2)在Rt△AOD中,∵∠AOD=90°,∠ADO=53°,OA=60,
(2)在Rt△AOD中,∵∠AOD=90°,∠ADO=53°,OA=60,
∴∠OAD=37°,
∴OD=OA•tan∠OAD≈60×$\frac{3}{4}$=45,
∴AD=$\sqrt{O{A}^{2}+A{D}^{2}}$=75,
∴BD=BO+OD=80+45=125.
在△ABD中,∵∠ABD=37°,∠ADB=53°,
∴∠BAD=180°-(∠ABD+∠ADB)=90°,
∴AB=$\sqrt{B{D}^{2}-A{D}^{2}}$=100.
设货船的速度为每小时x海里,则巡逻艇的速度为每小时(x+25)海里,
根据题意得$\frac{100+75}{x+25}$+$\frac{10}{60}$=$\frac{125}{x}$,
整理得x2+325x-18750=0,
解得x1=50,x2=-375(不合题意舍去).
经检验,x=50是原方程的解,也符合题意.
答:货船的速度为每小时50海里.
点评 此题考查了解直角三角形的应用-方向角问题,锐角三角函数,勾股定理,路程、时间与速度之间的关系的应用.作出辅助线构造直角三角形是解题的关键.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案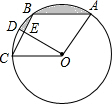 如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 4π-12$\sqrt{3}$ | B. | 4π-6$\sqrt{3}$ | C. | 4π | D. | 6π |
| A. | (-a)2•(-a)5 | B. | (-a)2•(-a5) | C. | (-a2)•(-a)5 | D. | (-a)•(-a)6 |
| A. | 300厘米 | B. | 250厘米 | C. | 200厘米 | D. | 150厘米 |
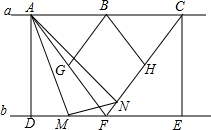 如图,直线a∥b,点A,B,C在直线a上,B是的AC中点,AC=4,分别过点A,C作直线b的垂线,垂足为D,E,F是直线b上的一个动点,连接AF,CF,若AF=CF.
如图,直线a∥b,点A,B,C在直线a上,B是的AC中点,AC=4,分别过点A,C作直线b的垂线,垂足为D,E,F是直线b上的一个动点,连接AF,CF,若AF=CF.