题目内容
18.计算(1)计算:($\frac{1}{2}$)-2+|$\sqrt{3}$-2|+3tan30°
(2)先化简,再求值:$\frac{1}{x+1}$-$\frac{3-x}{{x}^{2}-6x+9}$÷$\frac{{x}^{2}+x}{x-3}$,其中x=-$\frac{3}{2}$.
分析 (1)分别根据负整数指数幂的计算法则、绝对值的性质及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先算除法,再算加减,最后把x的值代入进行计算即可.
解答 解:(1)原式=4+2-$\sqrt{3}$+3×$\frac{\sqrt{3}}{3}$
=6-$\sqrt{3}$+$\sqrt{3}$
=6;
(2)原式=$\frac{1}{x+1}$-$\frac{3-x}{(x-3)^{2}}$•$\frac{x-3}{x(x+1)}$
=$\frac{1}{x+1}$+$\frac{1}{x(x+1)}$
=$\frac{x+1}{x(x+1)}$
=$\frac{1}{x}$,
当x=-$\frac{3}{2}$时,原式=$\frac{1}{-\frac{3}{2}}$=-$\frac{2}{3}$.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.若$\frac{1}{x+1}$在实数范围内有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>-1 | C. | x≠-1 | D. | x<-1 |
13.点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-x2+2x+c的图象上,则y1,y2,y3的大小关系是( )
| A. | y3>y2>y1 | B. | y3>y1=y2 | C. | y1>y2>y3 | D. | y1=y2>y3 |
8.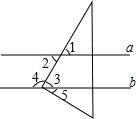 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )| A. | ∠2=60° | B. | ∠3=60° | C. | ∠4=120° | D. | ∠5=40° |
 用两种方法证明“三角形的外角和等于360°”.
用两种方法证明“三角形的外角和等于360°”. 一次函数y=ax+b和反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
一次函数y=ax+b和反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )

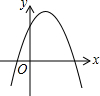

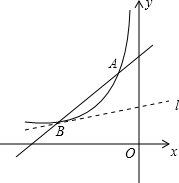 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象交于点A(-1,4)和点B(a,1).
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象交于点A(-1,4)和点B(a,1). 如图,BD是?ABCD的对角线,过点A作AE⊥BD,垂足为E,过点C作CF⊥BD,垂足为F.
如图,BD是?ABCD的对角线,过点A作AE⊥BD,垂足为E,过点C作CF⊥BD,垂足为F.