题目内容
9.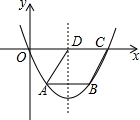 如图,在平面直角坐标系中,抛物线y=ax2-4ax(a>0)与x轴正半轴交于点C,这条抛物线的对称轴与x轴交于点D,以CD为边作菱形ABCD,若菱形ABCD的顶点A、B在这条抛物线上,则菱形ABCD的面积为2$\sqrt{3}$.
如图,在平面直角坐标系中,抛物线y=ax2-4ax(a>0)与x轴正半轴交于点C,这条抛物线的对称轴与x轴交于点D,以CD为边作菱形ABCD,若菱形ABCD的顶点A、B在这条抛物线上,则菱形ABCD的面积为2$\sqrt{3}$.
分析 抛物线的对称轴交AB于E点,如图,通过解方程ax2-4ax=0得到C(4,0),则抛物线的对称轴为直线x=2,则D(2,0),所以CD=2,根据菱形的性质得AB=CD=AD=2,AB∥CD,接着利用抛物线的对称性得到AE=BE=1,于是利用勾股定理可计算出DE,然后根据菱形的面积公式求解.
解答 解:抛物线的对称轴交AB于E点,如图,
当y=0时,ax2-4ax=0,解得x1=0,x2=4,则C(4,0),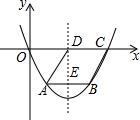
所以抛物线的对称轴为直线x=2,则D(2,0),
所以CD=4-2=2,
因为四边形ABCD为菱形,
所以AB=CD=AD=2,AB∥CD,
所以点A、B关于直线x=2对称,
所以AE=BE=1,
在Rt△ADE中,DE=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
所以菱形ABCD的面积=2×$\sqrt{3}$=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质和菱形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.表给出了y=x2+bx+c中x与y的一些对应值:
(1)设y=x2+bx+c,求b和c的值;并在表内的空格中填入适当的数;
(2)将抛物线y=x2+bx+c做怎样的平移,使它的顶点为坐标原点?
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
(2)将抛物线y=x2+bx+c做怎样的平移,使它的顶点为坐标原点?
20.关于x的方程mx2-4x+4=0有解,则m的取值为( )
| A. | m≥1 | B. | m≤1 | C. | m≥1且m≠0 | D. | m≤1且m≠0 |
1.已知△ABC的三边长都是整数,且AB=2,BC=6,则△ABC的周长可能是( )
| A. | 12 | B. | 14 | C. | 16 | D. | 17 |
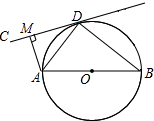 如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.
如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.