题目内容
4.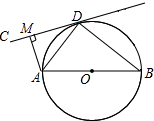 如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.
如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.(1)求证:∠ADC=∠ABD;
(2)若AD=2$\sqrt{3}$,⊙O的半径为3,求MD的长.
分析 (1)连接OD,由切线的性质和圆周角定理即可得到结果;
(2)由已知条件证得△ADM∽△ABD,即可得到结论.
解答 证明:(1)连接OD,如图: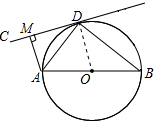
∵直线CD切⊙O于点D,
∴∠CDO=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADC+∠ADO=∠ADO+∠ODB=90°,
∴∠ADC=∠ODB,
∵OB=OD,
∴∠ODB=∠ADB,
∴∠ADC=∠ABD;
(2)∵⊙O的半径为3,AB=6,
∵∠ADB=90°,
∴DB═$\sqrt{A{B}^{2}-A{D}^{2}}=\sqrt{{6}^{2}-(2\sqrt{3})^{2}}=2\sqrt{6}$,
∵∠AMD=∠ADB=90°,∠ADC=∠ABD,
∴△ADM∽△ABD,
∴$\frac{DM}{BD}=\frac{AD}{AB}$,即$\frac{DM}{2\sqrt{6}}=\frac{2\sqrt{3}}{6}$
∴DM=2$\sqrt{2}$.
点评 本题考查了圆的切线性质,等腰三角形的性质,圆周角定理,解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
14.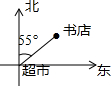 如图,书店在超市北偏东55°的方向上,那么以书店为参照点,超市的位置在( )
如图,书店在超市北偏东55°的方向上,那么以书店为参照点,超市的位置在( )
 如图,书店在超市北偏东55°的方向上,那么以书店为参照点,超市的位置在( )
如图,书店在超市北偏东55°的方向上,那么以书店为参照点,超市的位置在( )| A. | 书店的南偏西55°的方向上 | B. | 书店的南偏东55°的方向上 | ||
| C. | 书店的南偏西35°的方向上 | D. | 书店的南偏东35°的方向上 |
12.下列说法正确的是( )
| A. | 平分弦的直径垂直于弦 | B. | 相等的圆周角所对的弧相等 | ||
| C. | 三个点确定一个圆 | D. | 半圆或直径所对的圆周角是直角 |
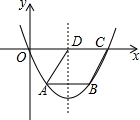 如图,在平面直角坐标系中,抛物线y=ax2-4ax(a>0)与x轴正半轴交于点C,这条抛物线的对称轴与x轴交于点D,以CD为边作菱形ABCD,若菱形ABCD的顶点A、B在这条抛物线上,则菱形ABCD的面积为2$\sqrt{3}$.
如图,在平面直角坐标系中,抛物线y=ax2-4ax(a>0)与x轴正半轴交于点C,这条抛物线的对称轴与x轴交于点D,以CD为边作菱形ABCD,若菱形ABCD的顶点A、B在这条抛物线上,则菱形ABCD的面积为2$\sqrt{3}$. 根据图中所表示的已知角的度数,可以求出∠α=50°.
根据图中所表示的已知角的度数,可以求出∠α=50°.