Question

5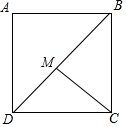．如图，在正方形ABCD中，M是对角线BD上一点，若AB=$\sqrt{2}$，则MD+2MC的最小值是$\sqrt{3}$+1，此时∠BMC=60度．

Answer 1

分析 如图将△ABP绕点A顺时针旋转60°得到△AEF，当E、F、P、C共线时，PA+PB+PC最小，作EM⊥DA交DA的延长线于M，ME的延长线交CB的延长线于N，在RT△ECN中理由勾股定理即可解决问题．

解答 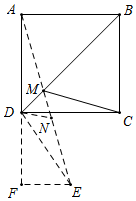解：如图，将△CDM绕点D顺时针旋转60°得到△EDN，连接AM，MN，则CM=EN，
∵MD=ND，∠MDN=60°，
∴△MDN是等边三角形，
∴MD=MN，
∵CM与AM关于BD对称，
∴AM=CM，
∴当E、N、M、A共线时，MD+2MC=MN+AM+NE=AE（最小），
此时，∠BMC=∠BMA=∠DMN=60°，
作EF⊥DA交AD的延长线于F，则∠F=90°，
由旋转可得∠CDE=60°，CD=ED=$\sqrt{2}$，
∴∠EDF=90°-60°=30°，
∴在Rt△DEF中，FE=$\frac{1}{2}$DE=$\frac{\sqrt{2}}{2}$，
∴DF=$\sqrt{D{E}^{2}-E{F}^{2}}$=$\frac{\sqrt{6}}{2}$，
∴AF=AD+DF=$\sqrt{2}$+$\frac{\sqrt{6}}{2}$，
∴Rt△AEF中，AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=$\sqrt{（\sqrt{2}+\frac{1}{2}\sqrt{6}）^{2}+（\frac{1}{2}\sqrt{2}）^{2}}$=$\sqrt{4+2\sqrt{3}}$=$\sqrt{（\sqrt{3}+1）^{2}}$=$\sqrt{3}$+1．
故答案为：$\sqrt{3}$+1，60°．

点评 本题主要考查了正方形的性质、轴对称的性质、旋转变换、等边三角形的判定与性质以及勾股定理等知识的综合应用，解题的关键是利用旋转添加辅助线，构造全等三角形，以及等边三角形，根据两点之间线段最短进行求解．