题目内容
16. 在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )
在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )| A. | π | B. | $\frac{2}{3}$π | C. | $\frac{3}{2}$π | D. | 2π |
分析 连接OO′交弧AB、AB分别于点C、D,根据切线的性质和垂径定理得AD的长,从而求得⊙O′的半径,利用周长公式求得圆的周长即可.
解答 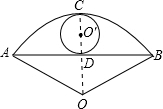 解:如图,
解:如图,
连接OO′交AB分别于点D,交弧AB于点C,
∵AB的长为2π,
∴由弧长公式得OA=3,
∵∠AOB=120°,
∴∠AOD=60°,
∵OC⊥AB,
∴∠ADO=90°,
∴∠OAD=30°,
∴OA=2OD,
∴OD=1.5,
∵OC=3,
∴CD=1.5,
∴CO′=$\frac{3}{4}$,
∴周长为2×$\frac{3}{4}$π=$\frac{3}{2}π$.
故选C.
点评 本题考查了切线的性质、垂径定理和弧长公式,是基础知识,要熟练掌握,解题的关键是能够正确的左侧辅助线.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
20.某股民在上周星期五买进某种股票,每股80元.如表是本周每日该股票的涨跌情况(单位:元):
星期五收盘时每股64元.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +6 | -4.5 | +5 | -3.5 | -7 |
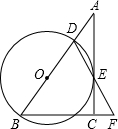 如图,在 Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点 F.
如图,在 Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点 F.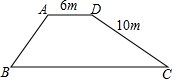 如图是一座堤坝的横断面,AB坡坡角为45°,DC坡坡度为1:2,其他数据如图所示,求BC的长(精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236)
如图是一座堤坝的横断面,AB坡坡角为45°,DC坡坡度为1:2,其他数据如图所示,求BC的长(精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236)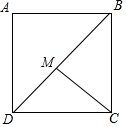 如图,在正方形ABCD中,M是对角线BD上一点,若AB=$\sqrt{2}$,则MD+2MC的最小值是$\sqrt{3}$+1,此时∠BMC=60度.
如图,在正方形ABCD中,M是对角线BD上一点,若AB=$\sqrt{2}$,则MD+2MC的最小值是$\sqrt{3}$+1,此时∠BMC=60度.