题目内容
2.解一元二次方程(1)(3x+2)2=24
(2)3x2-1=4x
(3)(2x+1)2=3(2x+1)
(4)x2+4x+2=0(配方法)
分析 (1)利用直接开方法求出x的值即可;
(2)先把方程整理为一元二次方程的一般形式,再用公式法求出x的值即可;
(3)先把方程化为两个因式积的形式,再求出x的值即可;
(4)把方程左边化为完全平方公式的形式,再用直接开方法求出x的值即可.
解答 解:(1)∵方程两边开方得,3x+2=±$\sqrt{24}$=±2$\sqrt{6}$,
∴x=$\frac{-2±2\sqrt{6}}{3}$,
∴x1=$\frac{-2+2\sqrt{6}}{3}$,x2=$\frac{-2-2\sqrt{6}}{3}$;
(2)∵原方程可化为3x2-4x-1=0,
∴a=3,b=-4,c=-1,
∴△=(-4)2-4×3×(-1)=2$\sqrt{7}$,
∴x=$\frac{4±2\sqrt{7}}{2×3}$=$\frac{4±2\sqrt{7}}{6}$,
∴x1=$\frac{2+\sqrt{7}}{3}$,x2=$\frac{2-\sqrt{7}}{3}$;
(3)∵原方程可化为(2x+1)(2x-2)=0,
∴2x+1=0或2x-2=0,
∴x1=-$\frac{1}{2}$,x2=1;
(4)∵原方程可化为x2+4x+4=2,即(x+2)2=2,
∴两边开方得,x+2=±$\sqrt{2}$,
∴x1=-2+$\sqrt{2}$,x2=-2-$\sqrt{2}$.
点评 本题考查的是利用因式分解法解一元二次方程,在解答此类问题时要根据方程的特点选择适当的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知△ABC中,∠C=90°,BC=3,AB=4,那么下列说法正确的是( )
| A. | sinB=$\frac{3}{5}$ | B. | cosB=$\frac{3}{4}$ | C. | tanB=$\frac{4}{3}$ | D. | cotB=$\frac{3}{4}$ |
11.四舍五入得到的近似数0.098,下列说法正确的是( )
| A. | 精确到万位 | B. | 精确到百分位 | C. | 精确到千分位 | D. | 精确到十分位 |
12.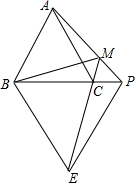 如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )
如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )
 如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )
如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.若∠ABM=40°,则∠APB=( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |
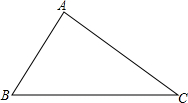 如图,已知△ABC,请你把它分成面积相等的四个小三角形,你能想出几种方法?
如图,已知△ABC,请你把它分成面积相等的四个小三角形,你能想出几种方法?
 △ABC中,AB=AC,∠CAB=120°,DE垂直平分AB,则∠ADC=60°.
△ABC中,AB=AC,∠CAB=120°,DE垂直平分AB,则∠ADC=60°.