题目内容
1.已知△ABC中,∠C=90°,BC=3,AB=4,那么下列说法正确的是( )| A. | sinB=$\frac{3}{5}$ | B. | cosB=$\frac{3}{4}$ | C. | tanB=$\frac{4}{3}$ | D. | cotB=$\frac{3}{4}$ |
分析 根据题意画出图形,先根据勾股定理求出AC的长,再由锐角三角函数的定义即可得出结论.
解答 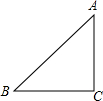 解:如图所示,∵△ABC中,∠C=90°,BC=3,AB=4,
解:如图所示,∵△ABC中,∠C=90°,BC=3,AB=4,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
A、sinB=$\frac{AC}{AB}$=$\frac{\sqrt{7}}{4}$≠$\frac{3}{5}$,故本选项错误;
B、cosB=$\frac{BC}{AB}$=$\frac{3}{4}$,故本选项正确;
C、tanB=$\frac{AC}{BC}$=$\frac{\sqrt{7}}{3}$≠$\frac{4}{3}$,故本选项错误;
D、cotB=$\frac{BC}{AC}$=$\frac{3}{\sqrt{7}}$=$\frac{3\sqrt{7}}{7}$≠$\frac{3}{4}$,故本选项错误.
故选B.
点评 本题考查的是锐角三角函数的定义,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
11.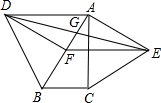 如图,分别以Rt△ABC的斜边AB,直角边AC为边向形外作等边△ABD和等边△ACE,F为AB 的中点.DE与AB相交于G,若∠BAC=30°,下列结论?:EF⊥AC;?AD=AE;?AD=4AG;?△DBF≌△EFA中,正确的有( )个.
如图,分别以Rt△ABC的斜边AB,直角边AC为边向形外作等边△ABD和等边△ACE,F为AB 的中点.DE与AB相交于G,若∠BAC=30°,下列结论?:EF⊥AC;?AD=AE;?AD=4AG;?△DBF≌△EFA中,正确的有( )个.
 如图,分别以Rt△ABC的斜边AB,直角边AC为边向形外作等边△ABD和等边△ACE,F为AB 的中点.DE与AB相交于G,若∠BAC=30°,下列结论?:EF⊥AC;?AD=AE;?AD=4AG;?△DBF≌△EFA中,正确的有( )个.
如图,分别以Rt△ABC的斜边AB,直角边AC为边向形外作等边△ABD和等边△ACE,F为AB 的中点.DE与AB相交于G,若∠BAC=30°,下列结论?:EF⊥AC;?AD=AE;?AD=4AG;?△DBF≌△EFA中,正确的有( )个.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列各式计算正确的是( )
| A. | 3x2-x2=3 | B. | 3a2+2a3=5a5 | C. | 3+x=3x | D. | 0.25ab-$\frac{1}{4}$ba=0 |
9.零上23℃,记作+23℃,零下8℃,可记作( )
| A. | 8 | B. | -8 | C. | 8℃ | D. | -8℃ |
16.($\sqrt{16}$)2的算术平方根是( )
| A. | 4 | B. | ±4 | C. | -4 | D. | 16 |
6.如下书写的四个美术字,其中为轴对称的是( )
| A. |  | B. |  | C. |  | D. |  |
13.下列各式从左到右的变形一定正确的是( )
| A. | $\frac{0.2a+b}{a+0.2b}=\frac{2a+b}{a+2b}$ | B. | $\frac{a}{2b}=\frac{ac}{2bc}$ | ||
| C. | $-\frac{x+1}{x-y}=\frac{x-1}{x-y}$ | D. | $\frac{{x-\frac{1}{2}y}}{{\frac{1}{2}x+y}}=\frac{2x-y}{x+2y}$ |
