题目内容
12.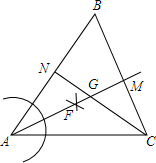 如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;
如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;(1)求证:∠BAM=∠CAM.
(2)作△ABC的角平分线CN交AM于G,求证:GM=GN.
分析 (1)连接QF、WF,根据SSS推出即可;
(2)过G作GZ⊥AB于Z,GP⊥BC于P,GO⊥AC于O,求出∠GZN=90°,GZ=GP=GO,∠GZB=∠GPB=90°,∠ZGP=120°,根据角平分线定义和三角形内角和定理求出∠NGM=∠AGC=120°,求出∠ZGN=∠MGP,根据ASA推出△ZGN≌△PGM即可.
解答 证明:(1)连接QF,WF,
由作法可知:AQ=AW,QF=WF,
∵在△AQF和△AWF中
$\left\{\begin{array}{l}{AQ=AW}\\{AF=AF}\\{FQ=FW}\end{array}\right.$
∴△AQF≌△AWF(SSS),
∴∠BAM=∠CAM;
(2)过G作GZ⊥AB于Z,GP⊥BC于P,GO⊥AC于O,
∵△ABC的角平分线CN交AM于G,
∴∠GZN=90°,GZ=GP=GO,∠GZB=∠GPB=90°,
∵∠B=60°,
∴∠ZGP=360°-90°-90°-60°=120°,
∵△ABC的角平分线CN交AM于G,∠B=60°,
∴∠GAC+∠GCA=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}×$(180°-60°)=60°,
∴∠NGM=∠AGC=180°-60°=120°,
即∠NGM=∠ZGP=120°,
∴都减去∠ZGM得:∠ZGN=∠MGP,
在△ZGN和△PGM中
$\left\{\begin{array}{l}{∠GZN=∠GPM=90°}\\{GZ=GP}\\{∠ZGN=∠MGP}\end{array}\right.$
∴△ZGN≌△PGM(ASA),
∴GM=GN.
点评 本题考查了角平分线定义及性质,全等三角形的性质和判定,三角形内角和定理的应用,能综合运用定理进行推理是解此题的关键.

| A. | 6$\sqrt{2}$ | B. | 10 | C. | 8 | D. | $\sqrt{31}$ |
 如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF,连接EF.
如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF,连接EF.
 已知,如图,AD=BC,AB=CD.
已知,如图,AD=BC,AB=CD. cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段MN的长是__________cm.
cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段MN的长是__________cm. 