题目内容
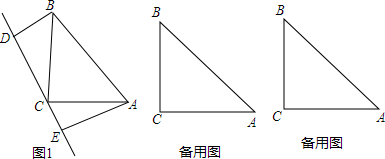
3.如图①,△ABC≌△DEF,将△ABC的顶点B和△DEF的顶点与E重合,把△DEF绕点B顺时针方向旋转,这时AC与DF相交于点O.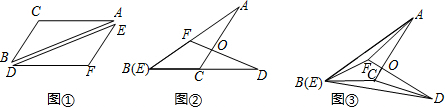
(1)当△DEF旋转至如图②位置,点B(E)、C、D在同一直线上时,∠AFD与∠DCA的数量关系是∠AFD=∠DCA.
(2)当△DEF继续旋转至如图③位置时,连接AF,CD,试证△ABF≌△DEC.
(3)在图③中,(1)中的结论还成立吗?连接BO、AD,BO与AD之间有怎样的位置关系?请分别说明理由.
分析 (1)根据全等三角形对应角相等可得∠A=∠D,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AOD=∠A+∠AFD,∠AOD=∠D+∠DCA,然后整理即可得解;
(2)根据全等三角形对应边相等可得AB=DE,BC=EF,根据全等三角形对应角相等可得∠ABC=∠DEF,∠BAC=∠EDF,然后推出∠ABF=∠DEC,利用边角边证明△ABF与△DEC全等,根据全等三角形对应角相等可得∠BAF=∠EDC,再推出∠FAC=∠CDF,然后利用三角形的外角性质列式即可得证;
(3)可以证明AO=DO,根据到线段两端点距离的点在线段垂直平分线得到BO⊥AD.
解答 解:(1)∵△ABC≌△DEF,
∴∠A=∠D,
又∵∠AOD=∠A+∠AFD,∠AOD=∠D+∠DCA,
∴∠AFD=∠DCA;
故答案为:∠AFD=∠DCA;
(2)∵△ABC≌△DEF,
∴AB=DE,BC=EF,∠ABC=∠DEF,∠BAC=∠EDF,
∴∠ABC-∠FBC=∠DEF-∠FBC,
即∠ABF=∠DEC,
在△ABF与△DEC中,
$\left\{\begin{array}{l}{AB=DE}\\{∠ABF=∠DEC}\\{BF=EC}\end{array}\right.$,
∴△ABF≌△DEC(SAS);
(3)(1)中的结论还成立,
∵△ABC≌△DEF,
∴AB=DE,BC=EF,∠ABC=∠DEF,
∴∠ABC-∠FBC=∠DEF-∠FBC,
∴∠ABF=∠DEC,
在△ABF和△DEC中,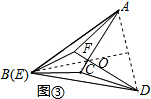
$\left\{\begin{array}{l}{AB=DE}\\{∠ABF=∠DEC}\\{BF=CE}\end{array}\right.$,
∴△ABF≌△DEC(SAS),
∴AF=CD,∠BAF=∠BDC,
∵∠BAC=∠BDF,
∴∠FAO=∠CDO,
在△AFO与△DCO中,$\left\{\begin{array}{l}{∠FAO=∠CDO}\\{∠AOF=∠DOC}\\{AF=DC}\end{array}\right.$,
∴△AFO≌△DCO,
∴∠AFD=∠DCO,AO=DO,
∴BO⊥AD.
点评 本题主要考查了全等三角形的判定与性质,利用旋转变换只改变图形的位置,不改变图形的形状与大小,找出两三角形全等的条件是解题的关键.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案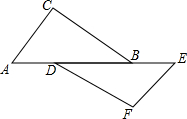 有如下命题:如图所示,点A、D、B、E在同一条直线上,则AC∥EF.判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.
有如下命题:如图所示,点A、D、B、E在同一条直线上,则AC∥EF.判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明. ______
______
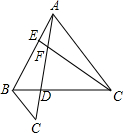 如图,已知等边△ABC,AE=BD,CE、AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:
如图,已知等边△ABC,AE=BD,CE、AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证: