题目内容
19.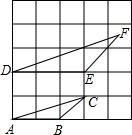 如图,在5×5的正方形方格中,△ABC和△DEF的顶点(除点F)都在边长为1的小正方形的顶点上,边DF,EF过小正方形顶点,则下列结论不正确的是( )
如图,在5×5的正方形方格中,△ABC和△DEF的顶点(除点F)都在边长为1的小正方形的顶点上,边DF,EF过小正方形顶点,则下列结论不正确的是( )| A. | ∠DEF=∠ABC | B. | △ABC和△DEF的面积比为3:2 | ||
| C. | △ABC的边AB上的高为1 | D. | △DEF的边DE上的高为$\frac{3}{2}$ |
分析 由图知∠DEF=90°+45°=135°,∠ABC=90°+45°=135°,得到∠DEF=∠ABC,故A正确;通过识图得到△ABC的边AB上的高为1,故C正确,由tanA=$\frac{1}{3}$,tanD=$\frac{1}{3}$,得到∠A=∠D,证得△ABC∽△DEF,求出相似比=$\frac{AB}{DE}$=$\frac{2}{3}$,得到△ABC和△DEF的面积比为4:9,故B错误;根据相似三角形的性质$\frac{AB边上的高}{DE边上的高}$=$\frac{2}{3}$,求出△DEF的边DE上的高为$\frac{3}{2}$,故D正确.
解答 解:由图知∠DEF=90°+45°=135°,∠ABC=90°+45°=135°,
∴∠DEF=∠ABC,故A正确;
∵△ABC的边AB上的高为1,故C正确,
∵tanA=$\frac{1}{3}$,tanD=$\frac{1}{3}$,
∴∠A=∠D,
∴△ABC∽△DEF,
∴相似比=$\frac{AB}{DE}$=$\frac{2}{3}$,
∴△ABC和△DEF的面积比为4:9,故B错误;
∴$\frac{AB边上的高}{DE边上的高}$=$\frac{2}{3}$,
∴△DEF的边DE上的高为$\frac{3}{2}$,故D正确.
故选B.
点评 本题考查了相似三角形的判定和性质,格点三角形,找准对应点是解题的关键.

练习册系列答案
相关题目
11.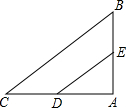 如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
 如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
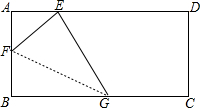 如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10,当折痕的另一端F在AB边上时,求△EFG的面积.
如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10,当折痕的另一端F在AB边上时,求△EFG的面积.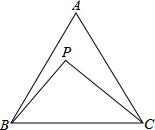 如图,等边三角形ABC中,点P在△ABC内部,且∠BPC=90°.若AB=7,CP=2$\sqrt{7}$,则tan∠ACP=$\frac{24-7\sqrt{3}}{49}$.
如图,等边三角形ABC中,点P在△ABC内部,且∠BPC=90°.若AB=7,CP=2$\sqrt{7}$,则tan∠ACP=$\frac{24-7\sqrt{3}}{49}$.