题目内容
10.如图1,P为△ABC内一点,连接PA、PB、PC,在△PAB,△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.(1)如图2,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE⊥CD,垂足为E,试说明E是△ABC的自相似点.
(2)在△ABC中,如图3,∠A<∠B<∠C,若△ABC的内心P是该三解形的自相似点,求该三角形三个内角的度数.

分析 (1)根据已知条件得出∠BEC=∠ACB,以及∠BCE=∠ABC,得出△BCE∽△ABC,即可得出结论;
(2)根据∠PBC=∠A,∠BCP=∠ABC=∠2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,即可得出各内角的度数.
解答 解:(1)在Rt△ABC中,∠ACB=90°,CD是AB上的中线,
∴CD=$\frac{1}{2}$AB,
∴CD=BD,
∴∠BCE=∠ABC,
∵BE⊥CD,∴∠BEC=90°,
∴∠BEC=∠ACB,
∴△BCE∽△ABC,
∴E是△ABC的自相似点;
(2)∵P是△ABC的内心,∴∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,
∵△ABC的内心P是该三角形的自相似点,
∴∠PBC=∠A,∠BCP=∠ABC=2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,
∴∠A+2∠A+4∠A=180°,
∴∠A=$\frac{180°}{7}$,
∴该三角形三个内角度数为:$\frac{180°}{7}$,$\frac{360°}{7}$,$\frac{720°}{7}$.
点评 此题主要考查了相似三角形的判定以及三角形的内心作法和作一角等于已知角,此题综合性较强,注意从已知分析获取正确的信息是解决问题的关键.

练习册系列答案
相关题目
6. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则图中相等的锐角有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则图中相等的锐角有( )
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则图中相等的锐角有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则图中相等的锐角有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
1. 小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日 6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2013年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图),同时将前4个月的用电量和相应电费制成表格(如表).根据上述信息,解答下列问题:
小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日 6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2013年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图),同时将前4个月的用电量和相应电费制成表格(如表).根据上述信息,解答下列问题:
(1)计算5月份的用电量和相应电费,将所得结果填入表中;
(2)小明家这5个月的月平均用电量呈上升趋势(选择“上升”或“下降”);这5个月每月电费呈下降趋势(选择“上升”或“下降”);
(3)小明预计7月份家中用电量很大,估计7月份用电可达500度,相应电费将达243元,请你根据小明的估计,计算出7月份小明家平时段用电量和谷时段用电量.
 小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日 6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2013年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图),同时将前4个月的用电量和相应电费制成表格(如表).根据上述信息,解答下列问题:
小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日 6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2013年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图),同时将前4个月的用电量和相应电费制成表格(如表).根据上述信息,解答下列问题:| 月用电量(度) | 电费(元) | |
| 1月 | 90 | 51.80 |
| 2月 | 92 | 50.85 |
| 3月 | 98 | 49.24 |
| 4月 | 105 | 48.55 |
| 5月 |
(2)小明家这5个月的月平均用电量呈上升趋势(选择“上升”或“下降”);这5个月每月电费呈下降趋势(选择“上升”或“下降”);
(3)小明预计7月份家中用电量很大,估计7月份用电可达500度,相应电费将达243元,请你根据小明的估计,计算出7月份小明家平时段用电量和谷时段用电量.
2.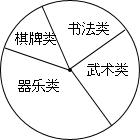 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数,他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图
某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数,他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图
请你根据以上图表提供的信息判断下列说法正确的有( )
①a=100,b=0.15;②在扇形统计图中器乐类所对应扇形的圆心角的度数是144°;③若该校七年级有学生1120人,大约有280名学生参加武术类校本课程.
 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数,他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图
某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数,他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图| 类别 | 频数(人数) | 频率 |
| 武术类 | 25 | 0.25 |
| 书画类 | 20 | 0.20 |
| 棋牌类 | 15 | b |
| 器乐类 | 40 | 0.40 |
| 合计 | a | 1.00 |
①a=100,b=0.15;②在扇形统计图中器乐类所对应扇形的圆心角的度数是144°;③若该校七年级有学生1120人,大约有280名学生参加武术类校本课程.
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
 如图,将-4,-3,-2,-1,0,1,2,3,4这9个数字填入图中的9个方格中,使得方格中,每行,每列,以及对角线上的3个数字之和都为0.
如图,将-4,-3,-2,-1,0,1,2,3,4这9个数字填入图中的9个方格中,使得方格中,每行,每列,以及对角线上的3个数字之和都为0.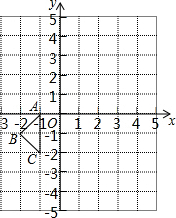 如图,△ABC的坐标分别为A(-1,0),B(-2,-1),C(-1,-2)
如图,△ABC的坐标分别为A(-1,0),B(-2,-1),C(-1,-2)