题目内容
6．
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，则图中相等的锐角有（ ）| A． | 1对 | B． | 2对 | C． | 3对 | D． | 4对 |
分析 根据直角三角形两锐角互余和同角的余角相等解答．
解答 
解：如图，∵∠ACB=90°，CD⊥AB，
∴∠1+∠A=90°，∠1+∠2=90°，
∠2+∠B=90°，
∴∠A=∠2，∠1=∠B，
即∠A=∠BCD，∠B=∠ACD，
相等的锐角有2对．
故选B．
点评 本题考查了直角三角形两锐角互余的性质，同角的余角相等的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
如图所示是边长为1的正方形网格，点A、B、C、D都在格点上．求图中阴影部分的面积．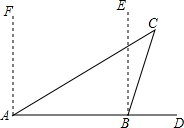
如图，一艘轮船上午8时在A处沿正东方向行驶，在A处测得灯塔C在北偏东60°方向上，行驶1小时后到达B处，在B处测得灯塔C在北偏东20°方向上．求△ABC各内角及∠DBC的度数．
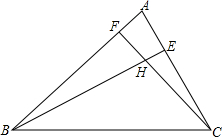在△ABC中，已知∠ABC=45°，∠ACB=60°，BE是AC上的高，CF交AB于点F，交BE于点H，且∠BHC=105°，△BFH是直角三角形吗？为什么？
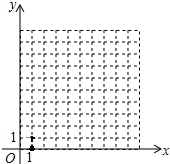如图，在平面直角坐标系中，一只蜘蛛P从点A（1，0），选择以下规定动作爬行