题目内容
15.Rt△ABC的两条直角边长分别为3cm、4cm,则该三角形的内切圆的面积为πcm2.分析 先利用勾股定理计算出斜边为5cm,再利用直角三角形的内切圆的半径=$\frac{a+b-c}{2}$(a、b为直角边,c为斜边)计算出该三角形的内切圆的半径,然后利用圆的面积公式求解.
解答 解:斜边=$\sqrt{{3}^{2}+{4}^{2}}$=5,
则该三角形的内切圆的半径=$\frac{3+4-5}{2}$=1,
所以该三角形的内切圆的面积=π•12=π(cm2).
故答案为πcm2.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.记住直角三角形的内切圆的半径=$\frac{a+b-c}{2}$(a、b为直角边,c为斜边).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

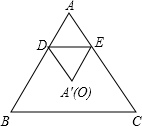 如图,等边三角形ABC中,AB=3,点D,E分别在AB,AC上,且DE∥BC,沿直线DE折叠△ABC,当点A的对应点A′与△ABC的中心O重合时,折痕DE的长为1.
如图,等边三角形ABC中,AB=3,点D,E分别在AB,AC上,且DE∥BC,沿直线DE折叠△ABC,当点A的对应点A′与△ABC的中心O重合时,折痕DE的长为1.