题目内容
 如图,由24个边长为1的正方形组成4×6的网格.若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是
如图,由24个边长为1的正方形组成4×6的网格.若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是考点:相似三角形的性质
专题:网格型
分析:易求△ABC的面积,因为△A′B′C′∽△ABC(相似比不是1),利用相似三角形的性质:面积比等于相似比的平方即可求出△A′B′C′的面积.
解答:
 解:∵△ABC的三边为
解:∵△ABC的三边为
,
,
,
∴△A′B′C′三边可能为2,
,
;2
,2
,2
;
,5,5;4,2
,2
;
∵△A′B′C′∽△ABC,S△ABC=2×2-2×
×2×1-
×1×1=1.5,
∴△A′B′C′的面积是1.5×(
)2=3;1.5×22=6;1.5×(
)2=7.5;1.5×(2
)2=12.
故答案为:3,6,7.5,12.
 解:∵△ABC的三边为
解:∵△ABC的三边为| 2 |
| 5 |
| 5 |
∴△A′B′C′三边可能为2,
| 10 |
| 10 |
| 2 |
| 5 |
| 5 |
| 10 |
| 10 |
| 10 |
∵△A′B′C′∽△ABC,S△ABC=2×2-2×
| 1 |
| 2 |
| 1 |
| 2 |
∴△A′B′C′的面积是1.5×(
| 2 |
| 5 |
| 2 |
故答案为:3,6,7.5,12.
点评:本题考查对相似三角形性质的理解,相似三角形面积比等于相似比的平方.解题的关键是根据△ABC的三边长找到它们的对应边最长的长度为4,2
,2
.
| 10 |
| 10 |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等.
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等.
| A、①②③ | B、③④⑤ |
| C、①②⑤ | D、②④⑤ |
 下面如图是以右边四个图中的哪一个绕着直线旋转一周得到的( )
下面如图是以右边四个图中的哪一个绕着直线旋转一周得到的( )A、 |
B、 |
C、 |
D、 |
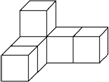 由6个大小相同的正方体搭成的几何体如图所示,关于它的视图,说法正确的是( )
由6个大小相同的正方体搭成的几何体如图所示,关于它的视图,说法正确的是( )| A、主视图的面积最大 |
| B、左视图的面积最大 |
| C、俯视图的面积最大 |
| D、三个视图的面积一样大 |
如图,不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
某日,北京市的最低气温是-10℃,杭州市的最低气温是-1℃,则这一天北京的最低气温比杭州的最低气温低( )
| A、-11℃ | B、-9℃ |
| C、11℃ | D、9℃ |
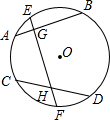 已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证:
已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证:
 李爷爷借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园,想在里面种些花草,篱笆只围AB、BC两边.
李爷爷借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园,想在里面种些花草,篱笆只围AB、BC两边.