题目内容
6．若实数a，b满足a+b2=1，则a2+b2的最小值是$\frac{3}{4}$．分析 由a+b2=1，得出b2=1-a，代入得到a2+b2=a2+1-a，利用配方法即可求解．
解答 解：∵a+b2=1，
∴b2=1-a，
∴a2+b2=a2+1-a=（a-$\frac{1}{2}$）2+$\frac{3}{4}$≥$\frac{3}{4}$，
∴当a=$\frac{1}{2}$时，a2+b2有最小值$\frac{3}{4}$．
故答案为$\frac{3}{4}$．
点评 本题考查了配方法的应用，非负数的性质，将b2=1-a代入得到a2+b2=a2+1-a是解题的关键．
练习册系列答案
相关题目
16．
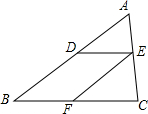如图，在△ABC中，DE∥BC，若AD=1，BD=2，则$\frac{DE}{BC}$的值为（ ）
如图，在△ABC中，DE∥BC，若AD=1，BD=2，则$\frac{DE}{BC}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{2}{3}$ |
如图，要使AB∥CD，只需要添加一个条件，这个条件是∠ABD=∠BDC（填一个你认为正确的条件即可）．
15．
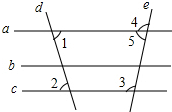如图，下列说法错误的是（ ）
如图，下列说法错误的是（ ）| A． | 若∠3=∠2，则b∥c | B． | 若∠3+∠5=180°，则a∥c | ||
| C． | 若∠1=∠2，则a∥c | D． | 若a∥b，b∥c，则a∥c |