题目内容
16. 如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
分析 根据平行四边形对角相等,求出∠BCD,再根据邻补角的定义求出∠MCD即可.
解答 解:∵四边形ABCD是平行四边形,
∴∠A=∠BCD=135°,
∴∠MCD=180°-∠DCB=180°-135°=45°.
故选A.
点评 本题考查平行四边形的性质、邻补角定义等知识,解题的关键是熟练掌握平行四边形性质,属于基础题,中考常考题型.

练习册系列答案
相关题目
6.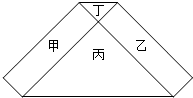 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
11.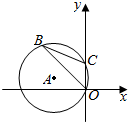 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )| A. | $\frac{1}{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$ |
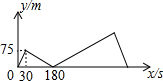 甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是175米.
甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是175米.
 =__________(a<0)
=__________(a<0) ;
;