题目内容
12. 如图是一把含30°角的三角尺,外边AB=8,内边与外边的距离都是1,那么EP的长度是( )
如图是一把含30°角的三角尺,外边AB=8,内边与外边的距离都是1,那么EP的长度是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | $\frac{5}{2}$ | D. | 6-2$\sqrt{3}$ |
分析 解直角三角形求出AC,延长EF交BC于N,延长FE交AB于M,过E作EG⊥AB于G,证△BMN∽△BAC,求出MN,解直角三角形求出ME,即可求出答案.
解答 解:如图,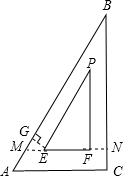
∵在Rt△BAC中,∠C=90°,AB=8,∠B=30°,∠A=60°,
∴AC=4,BC=AC×tan60°=4$\sqrt{3}$,
延长EF交BC于N,延长FE交AB于M,过E作EG⊥AB于G,
∵EF∥AC,
∴∠BMN=∠A=60°,△BMN∽△BAC,
∴$\frac{MN}{AC}$=$\frac{BN}{BC}$,
∴$\frac{MN}{4}$=$\frac{4\sqrt{3}-1}{4\sqrt{3}}$,
解得:MN=4-$\frac{\sqrt{3}}{3}$,
∵GE⊥AB,
∴∠EGM=90°,
∵∠GME=60°,GE=1,
∴ME=$\frac{GE}{sin60°}$=$\frac{2\sqrt{3}}{3}$,
∴EF=MN-ME-FN=4-$\frac{\sqrt{3}}{3}$-1-$\frac{2}{3}$$\sqrt{3}$=3-$\sqrt{3}$,
∴EP=2EF=6-2$\sqrt{3}$.
故选:D.
点评 本题考查了解直角三角形和相似三角形的性质和判定的应用,特殊角的三角函数值,关键是求出NF、MN、EM的值.

练习册系列答案
相关题目
2.某商场花了9万元从厂家购买了A型、B型两种型号的电视机共50台,其中A型电视机的进价为每台1500,B型电视机的进价为每台2500元.
(1)若设购买了A型电视机x台,B型电视机y台,请完成下列表格:
(2)在(1)的基础上,通过列二元一次方程组求该商场购买A型和B型电视机各多少台?
(3)若商场A型电视机的售价为每台1700元,B型电视机的售价为每台2800元,不考虑其他因素,那么销售完这50台电视机该商场可获利多少元?
(1)若设购买了A型电视机x台,B型电视机y台,请完成下列表格:
| 进价(元/台) | 购买数量(台) | 购买数量(元) | |
| A型 | 1500 | x | |
| B型 | 2500 | y |
(3)若商场A型电视机的售价为每台1700元,B型电视机的售价为每台2800元,不考虑其他因素,那么销售完这50台电视机该商场可获利多少元?
17. 如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
 如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )| A. | 伟 | B. | 大 | C. | 的 | D. | 国 |
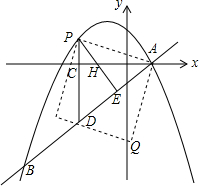 如图,在平面直角坐标系中,直线y=kx+n(k≠0)与抛物线y=-$\frac{1}{4}{x^2}$+bx+c交于A、B两点,点A在x轴上,OA=2,点B的横坐标为-8,且tan∠OAB=$\frac{3}{4}$.
如图,在平面直角坐标系中,直线y=kx+n(k≠0)与抛物线y=-$\frac{1}{4}{x^2}$+bx+c交于A、B两点,点A在x轴上,OA=2,点B的横坐标为-8,且tan∠OAB=$\frac{3}{4}$. 看图.项空:
看图.项空: 如图,在等边△ABC中,AC=9,点O、P、D分别在AC、AB、BC上,AO=3,OP=OD,且∠DOP=60°,则AP的长是6.
如图,在等边△ABC中,AC=9,点O、P、D分别在AC、AB、BC上,AO=3,OP=OD,且∠DOP=60°,则AP的长是6. 某城市有座古塔,如图是古塔底部的建筑平面图,要测量这座古塔外墙底部∠ABC的度数,请你运用学过的知识设计比一种测量方案,并说明理由.
某城市有座古塔,如图是古塔底部的建筑平面图,要测量这座古塔外墙底部∠ABC的度数,请你运用学过的知识设计比一种测量方案,并说明理由.