题目内容
11.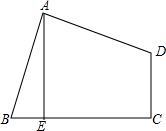 如图所示,在四边形ABCD中.AB=AD,∠BAD=∠C=90°,BC=5,CD=3,过点A作AE⊥BC,垂足为点E,请你利用旋转变换求AE的长.
如图所示,在四边形ABCD中.AB=AD,∠BAD=∠C=90°,BC=5,CD=3,过点A作AE⊥BC,垂足为点E,请你利用旋转变换求AE的长.
分析 过点A作AF⊥CD交CD延长线于F,可以证明△ABE≌△ADF,即可证明四边形AECF是正方形,据此即可求解.
解答  解:过点A作AF⊥CD交CD延长线于F,
解:过点A作AF⊥CD交CD延长线于F,
∵AE⊥BC,AF⊥CD,∠C=90,
∴四边形AECF是矩形.
∴∠EAF=90,∠AEB=∠AFC=90,
∴∠EAD+∠DAF=90.
∵∠BAD=90,
∴∠EAD+∠BAE=90,
∴∠DAF=∠BAE.
∴在△ABE和△ADF中,
$\left\{\begin{array}{l}{∠AFC=∠AEB}\\{∠BAE=∠FAD}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADF (AAS).
∴AF=AE,BE=DF,
∴正方形AECF.
∴AE=CE=CF,
∴BE=BC-CE=BC-AE=5-AE,DF=CF-CD=AE-CD=AE-3,
∴5-AE=AE-3,
∴AE=4.
点评 本题考查了全等三角形的判定与性质,正确作出辅助线,证明△ABE≌△ADF是解决本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
19.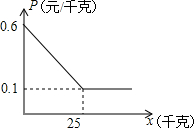 某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.
某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.
(1)求出价格P(元/千克)与卖给餐厅的土豆数量x(千克)之间的关系式.
(2)设每天小贩从批发市场批发土豆的数量为x(千克),每月所得的毛利润为W(元).
①根据具体的x(千克)的值,填写下表:
②该小贩每天从批发市场买进多少千克土豆才能使每月所获得利润最大?最多可赚多少钱?
 某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.
某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.(1)求出价格P(元/千克)与卖给餐厅的土豆数量x(千克)之间的关系式.
(2)设每天小贩从批发市场批发土豆的数量为x(千克),每月所得的毛利润为W(元).
①根据具体的x(千克)的值,填写下表:
| 所批发土豆的数量x(千克) | 70 | 90 | 100 |
| 每月所得毛利润W(元) | 420 | 540 | 570 |
 如图,平行四边形ABCD中,如果把图中线段都画成有向线段,那么在这些有向线段所表示的向量中,用符号把符合下列要求的向量表示出来:
如图,平行四边形ABCD中,如果把图中线段都画成有向线段,那么在这些有向线段所表示的向量中,用符号把符合下列要求的向量表示出来: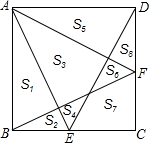 如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.
如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.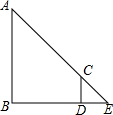 古塔测高有一座古塔,不知有多高,测得影长为11.3米,现将一长为0.8米的竹竿直立,使其影子的末端与塔影的末端重合,测得竹竿的影长为0.2米,求塔高.
古塔测高有一座古塔,不知有多高,测得影长为11.3米,现将一长为0.8米的竹竿直立,使其影子的末端与塔影的末端重合,测得竹竿的影长为0.2米,求塔高.