题目内容
8.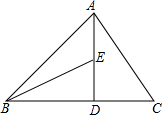 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.(1)求证:△BDE≌△ADC;
(2)若BC=8.4,tanC=$\frac{5}{2}$,求DE的长.
分析 (1)由AD⊥BC可得∠ADB=∠ADC=90°,又∠ABC=45°易得∠ABC=∠BAD,可得AD=BD,由SAS定理可得△BDE≌△ADC;
(2)设DE=x,因为tanC=$\frac{5}{2}$可得AD=2.5x,可得BC=3.5x,由BC=8.4,可解得x,可得DE.
解答 (1)证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠ABC=45°,
∴∠BAD=45°,
∴∠ABC=∠BAD,
∴AD=BD,
在△BDE和△ADC中,
$\left\{\begin{array}{l}{BD=AD}\\{∠EDB=∠ADC}\\{DE=DC}\end{array}\right.$,
∴△BDE≌△ADC(SAS);
(2)解:设DE=x,
∵DE=DC,
∴DC=x,
∵tanC=$\frac{5}{2}$,
∴AD=2.5x,
∵AD=BD,
∴BD=2.5x,
∴BC=BD+CD=3.5x,
∵BC=8.4,
∴x=2.4,
DE=2.4.
点评 本题主要考查了全等三角形的性质和判定,利用方程思想是解答此题的关键.

练习册系列答案
相关题目
19.下列计算正确的是( )
| A. | 2a2•a=3a3 | B. | (2a)2÷a=4a | C. | (-3a)2=3a2 | D. | (a-b)2=a2-b2 |
3.计算$\frac{1}{2}$-$\frac{1}{2}$×3的结果是( )
| A. | 0 | B. | 1 | C. | -2 | D. | -1 |
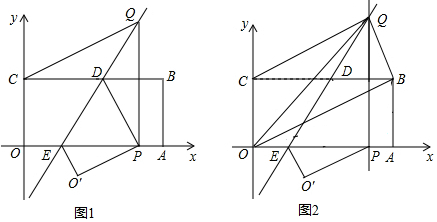
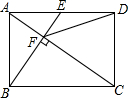
13. 已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为( )
已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为( )
 已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为( )
已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为( )| A. | a-1 | B. | a | C. | $\sqrt{{a}^{2}-1}$ | D. | $\sqrt{{a}^{2}+2a}$ |
 在矩形ABCD中,点E为AD的中点,连接BE、AC,AC⊥BE于点F,连接DF,则下列结论正确的有②③④.
在矩形ABCD中,点E为AD的中点,连接BE、AC,AC⊥BE于点F,连接DF,则下列结论正确的有②③④.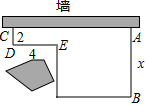 用一段长为32m的篱芭绕过障碍物围成一个菜园,菜园一边靠墙.如图,已知CD=2m,DE=4m,设AB=x(m)(2<x<14),菜园面积为y(m2),请回答下列问题:
用一段长为32m的篱芭绕过障碍物围成一个菜园,菜园一边靠墙.如图,已知CD=2m,DE=4m,设AB=x(m)(2<x<14),菜园面积为y(m2),请回答下列问题: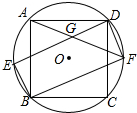 正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G.
正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G.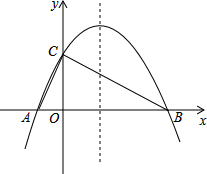 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).