题目内容
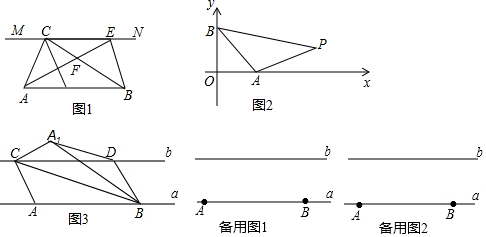
4.如图,A、B是直线a上的两个定点,点C、D在直线b上运动(点C在点D的左侧),AB=CD=4,已知a∥b,且a与b间的距离为$\sqrt{3}$,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.(1)当A1、D两点重合时,在图1中画出相应图形,并直接给出AC的长度;
(2)当A1、D两点不重合时,如图2,连接A1D,请直接说出A1D与BC的位置关系;
(3)如图3,以A1、C、B、D为顶点的四边形的面积是否存在最大值,若存在,求出该四边形的面积的最大值;若不存在,请说明理由.
分析 (1)由△ABC沿BC折叠得△A1BC,AC=CD,即可;
(2)根据折叠的性质得到∠A1BC=∠ABC,根据平行线的性质得到∠A1BC=∠BCD,推出∠BA1D=∠A1DC,根据平行线的判定定理即可得到结论;
(3)当以A1、C、B、D为顶点的四边形是矩形时,四边形的面积的最大,Ⅰ、过点C作CE⊥AB,垂足为点E,根据矩形的性质得到∠ACB=∠A1CB=90°,根据相似三角形的性质得到CE2=AE×BE,列方程得到A1C,BC,于是得到结论;Ⅱ、如图2,当BC⊥AB时,A1点在AB上,根据矩形的面积公式即可得到结论.
解答 解:(1)当A1D两点重合时,
由△ABC沿BC折叠得△A1BC,
∴AC=CD,
∵CD=4,
∴AC=4
故答案为4;
(2)A1D∥BC,
理由如下:设A1B、CD相交于点O.
由翻折可知:∠A1BC=∠ABC,
∵a∥b,
∴∠A1BC=∠BCD,
∴OC=OB,
∵AB=A1B=CD,
∴A1O=DO,
∴∠BA1D=∠A1DC,
∵∠BA1D+∠A1DC=∠A1BC+∠BCD=∠BOD,
∴2∠BA1D=2∠A1BC,
即∠BA1D=∠A1BC,
∴A1D∥BC;
(3) ∵C、D是动点,AB=A1B=4,
∵C、D是动点,AB=A1B=4,
∴A1运动的轨迹是以B为圆心,4为半径的部分圆弧,当A1处在直线a以下的圆弧部分并且A1B⊥直线a时,以A1、C、B、D为顶点的四边形的面积的最大,
∵A1B⊥AB,
∴△AA1B是等腰直角三角形,
∴BC=$\sqrt{6}$,
∵BC∥A1D,
∴四边形BA1DC是等腰梯形,
∴梯形的高为2$\sqrt{2}$,
∴A1B=4$\sqrt{2}$+$\sqrt{6}$,
∴S${\;}_{四边形{A}_{1}CBD}$=$\frac{1}{2}$(4$\sqrt{2}$+2$\sqrt{6}$)×2$\sqrt{2}$=8+4$\sqrt{3}$.
点评 此题主要考查了相似三角形的性质和判定,对折的性质,矩形的性质,平行线的判定和性质,建立方程是解本题的关键.

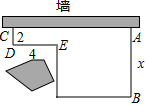 用一段长为32m的篱芭绕过障碍物围成一个菜园,菜园一边靠墙.如图,已知CD=2m,DE=4m,设AB=x(m)(2<x<14),菜园面积为y(m2),请回答下列问题:
用一段长为32m的篱芭绕过障碍物围成一个菜园,菜园一边靠墙.如图,已知CD=2m,DE=4m,设AB=x(m)(2<x<14),菜园面积为y(m2),请回答下列问题: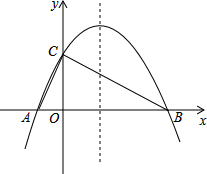 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).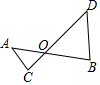 如图,已知直线AB与CD相交于点O,且∠DOB=∠ODB,若∠ODB=50°,则∠AOC的度数为50°;∠CAO是(填“是”或“不是”)∠AOC的同旁内角.
如图,已知直线AB与CD相交于点O,且∠DOB=∠ODB,若∠ODB=50°,则∠AOC的度数为50°;∠CAO是(填“是”或“不是”)∠AOC的同旁内角.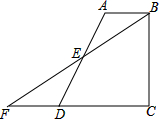 如图,在四边形ABCD中,AB∥CD,BC⊥CD,垂足为点C,E是AD的中点,连接BE并延长交CD的延长线于点F.
如图,在四边形ABCD中,AB∥CD,BC⊥CD,垂足为点C,E是AD的中点,连接BE并延长交CD的延长线于点F.