题目内容
10.已知a=-$\frac{1}{2}$,b=-$\frac{1}{5}$,c=-$\frac{1}{5}$,d=$\frac{3}{4}$,求a-b+c-d的值.分析 将a、b、c、d的值代入代数式进行计算即可得解.
解答 解:当a=-$\frac{1}{2}$,b=-$\frac{1}{5}$,c=-$\frac{1}{5}$,d=$\frac{3}{4}$时,
a-b+c-d=-$\frac{1}{2}$-(-$\frac{1}{5}$)+(-$\frac{1}{5}$)-$\frac{3}{4}$,
=-$\frac{1}{2}$+$\frac{1}{5}$-$\frac{1}{5}$-$\frac{3}{4}$,
=-$\frac{1}{2}$-$\frac{3}{4}$,
=-$\frac{5}{4}$.
点评 本题考查了代数式求值,比较简单,主要利用了有理数的加法与减法运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若a、b、c都不为0,化简$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{{|{abc}|}}{abc}$结果有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
2.在Rt△ABC中,∠A=30°,则另一个锐角,∠B=( )
| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
19. 如图,在单位长度为1的数轴上有A,B,C,D四点,分别表示整数a,b,c,d,且d-a-c=6,则原点的位置为( )
如图,在单位长度为1的数轴上有A,B,C,D四点,分别表示整数a,b,c,d,且d-a-c=6,则原点的位置为( )
 如图,在单位长度为1的数轴上有A,B,C,D四点,分别表示整数a,b,c,d,且d-a-c=6,则原点的位置为( )
如图,在单位长度为1的数轴上有A,B,C,D四点,分别表示整数a,b,c,d,且d-a-c=6,则原点的位置为( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
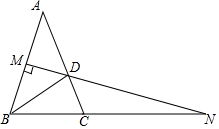 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交BC的延长线于点N,交AC于点D,连接BD,AD=6,
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交BC的延长线于点N,交AC于点D,连接BD,AD=6, 用长为8米的绳子围成一个矩形ABCD,使得∠ACB=32°,则边BC的长约为2.41米.(用科学计算器计算,结果精确到0.01米)
用长为8米的绳子围成一个矩形ABCD,使得∠ACB=32°,则边BC的长约为2.41米.(用科学计算器计算,结果精确到0.01米)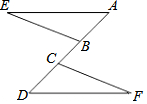 如图,已知A、B、C、D在一条直线上,EB=FC,EB∥FC,∠E=∠F,试说明:
如图,已知A、B、C、D在一条直线上,EB=FC,EB∥FC,∠E=∠F,试说明: