题目内容
5. 用长为8米的绳子围成一个矩形ABCD,使得∠ACB=32°,则边BC的长约为2.41米.(用科学计算器计算,结果精确到0.01米)
用长为8米的绳子围成一个矩形ABCD,使得∠ACB=32°,则边BC的长约为2.41米.(用科学计算器计算,结果精确到0.01米)
分析 由题意知AB=4-BC,在Rt△ABC中由tan∠ACB=$\frac{AB}{BC}$,即tan32°=$\frac{4-BC}{BC}$可求得BC.
解答 解:∵AB+BC=4,
∴AB=4-BC,
在Rt△ABC中,∵∠ACB=32°,
∴tan∠ACB=$\frac{AB}{BC}$,即tan32°=$\frac{4-BC}{BC}$,
解得:BC=$\frac{4}{1+tan32°}$≈2.41(米),
故答案为:2.41.
点评 本题主要考查解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
17.用计算器求(-2)6的值,下列按键顺序正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
14.抛物线y=3(x+1)2-4的顶点坐标是( )
| A. | (1,4) | B. | (1,-4) | C. | (-1,4) | D. | (-1,-4) |
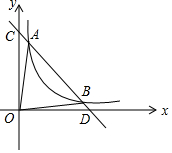 如图,已知一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,6),B(3,n)两点.
如图,已知一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,6),B(3,n)两点.