Question

在直角坐标系中，以原点为圆心，4为半径作圆，该圆上到直线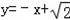的距离等于2的点共有（　　）

A．1个  B．2个   C．3个  D．4个

　

Answer 1

D【考点】垂径定理；坐标与图形性质；三角形内角和定理；勾股定理；直线与圆的位置关系．

【专题】计算题．

【分析】过O作OH⊥AB，求出O到直线的距离，和圆的半径比较得出圆于直线相交，且圆心到直线的距离是1，画出图形，得出在直线的两旁到直线的距离等于2的点有4个点，即可得出答案．

【解答】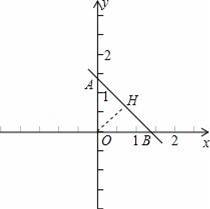

解：过O作OH⊥AB于H，

y=﹣x+，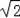

∵当x=0时，y=，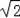

当y=0时，x=，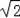

∴AO=OB=，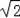

由勾股定理得：AB=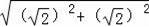=2，

由三角形的面积公式得：AB×OH=AO×OB，

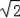
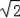
即2OH=×=2，

解得：OH=1＜4，

即直线与圆相交，

如图：

在直线的两旁到直线的距离等于2的点有4个点（E、F、G、N），

故选D．

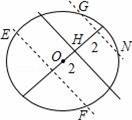
【点评】本题考查了直线与圆的位置关系和三角形的面积的应用，关键是求出直线与圆的位置关系和画出第二个图形，主要考查学生的理解能力和推理能力，题目有一定的难度，注意：不要漏解啊．