题目内容
如图，点C、D在线段AB上，△PCD是等边三角形，且△ACP∽△PDB，求∠APB的度数．
【考点】相似三角形的性质．
【分析】根据等边三角形的性质得到∠PCD=60°，根据相似三角形的判定定理证明△ACP∽△ABP，根据相似三角形的性质得到答案．
【解答】解：∵△PCD是等边三角形，
∴∠PCD=60°，
∴∠ACP=120°，
∵△ACP∽△PDB，
∴∠APC=∠B，又∠A=∠A，
∴△ACP∽△ABP，
∴∠APB=∠ACP=120°．
【点评】本题考查的是相似三角形的判定和性质，掌握相似三角形的对应角相等是解题的关键．
练习册系列答案
相关题目
.
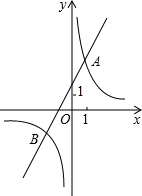
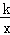的图象与一次函数y2=ax+b的图象交于点A（1，4）和点（m，﹣2），则满足y1＞y2的自变量x的取值范围是__________．
