题目内容
16.下列分式运算,正确的是( )| A. | ${(\frac{2b}{3a})^2}=\frac{{2{b^2}}}{{3{a^2}}}$ | B. | $\frac{{{x^2}-4}}{x-2}=x-2$ | C. | $2x•\frac{1}{2x}=\frac{1}{{4{x^2}}}$ | D. | $\frac{1}{x-y}+\frac{1}{y-x}=0$ |
分析 根据各个选项中的式子可以计算出正确的结果,从而可以解答本题.
解答 解:∵$(\frac{2b}{3a})^{2}=\frac{4{b}^{2}}{9{a}^{2}}$,故选项A错误,
∵$\frac{{x}^{2}-4}{x-2}=\frac{(x+2)(x-2)}{x-2}=x+2$,故选项B错误,
∵$2x•\frac{1}{2x}=1$,故选项C错误,
∵$\frac{1}{x-y}+\frac{1}{y-x}=\frac{1}{x-y}-\frac{1}{x-y}=0$,故选项D正确,
故选D.
点评 本题考查分式的混合运算,解答本题的关键是明确分式混合的计算方法.

练习册系列答案
相关题目
1. 如图是某几何体的三种视图,则这个几何体是( )
如图是某几何体的三种视图,则这个几何体是( )
 如图是某几何体的三种视图,则这个几何体是( )
如图是某几何体的三种视图,则这个几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 球 | D. | 四棱锥 |
6.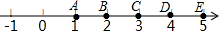 如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )
如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )
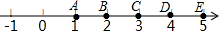 如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )
如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )| A. | 点A和点B | B. | 点B和点C | C. | 点C和点D | D. | 点D和点E |
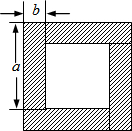 如图所示的是用四块完全相同的小长方形拼成的一个“回形”正方形.
如图所示的是用四块完全相同的小长方形拼成的一个“回形”正方形.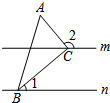 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2等于130度.
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2等于130度.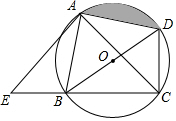 如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.
如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.