题目内容
4.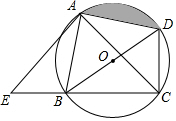 如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.
如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.(1)求证:BE=CD;
(2)如果AD=$\sqrt{2}$,求图中阴影的面积.
分析 (1)由BD为⊙O的直径,得到∠BAC=90°,根据圆周角定理得到∠ADB=∠ACB=45°,推出△ADE与△ABD是等腰直角三角形,根据全等三角形的性质即可得到结论;
(2)连接AO,则∠AOD=90°,根据勾股定理得到AO=OD=1,根据图形的面积公式即可得到结论.
解答 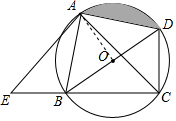 解:(1)∵BD为⊙O的直径,
解:(1)∵BD为⊙O的直径,
∴∠BAC=90°,
∵∠ACB=45°,
∴∠ADB=∠ACB=45°,
∵AE⊥AC,
∴△ADE与△ABD是等腰直角三角形,
∴AE=AC,AB=AD,∠EAC=∠BAD=90°,
∴∠EAB=∠CAD,
在△ABE与△ADC中,$\left\{\begin{array}{l}{AE=AC}\\{∠EAB=∠CAD}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADC,
∴BE=CD;
(2)连接AO,则∠AOD=90°,
∵AD=$\sqrt{2}$,
∴AO=OD=1,
∴S阴影=S扇形-S△AOD=$\frac{90•π×{1}^{2}}{360}$-$\frac{1}{2}$×1×1=$\frac{π}{4}$-$\frac{1}{2}$.
点评 本题考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,扇形的面积的计算,圆周角定理,熟练掌握圆周角定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列分式运算,正确的是( )
| A. | ${(\frac{2b}{3a})^2}=\frac{{2{b^2}}}{{3{a^2}}}$ | B. | $\frac{{{x^2}-4}}{x-2}=x-2$ | C. | $2x•\frac{1}{2x}=\frac{1}{{4{x^2}}}$ | D. | $\frac{1}{x-y}+\frac{1}{y-x}=0$ |
14.在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有凫(凫:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,下面所列方程正确的是( )
| A. | (9-7)x=1 | B. | (9-7)x=1 | C. | ($\frac{1}{7}$+$\frac{1}{9}$)x=1 | D. | ($\frac{1}{7}$-$\frac{1}{9}$)x=1 |
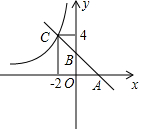 如图,一条直线分别交x轴、y轴于A、B两点,交反比例函数y=$\frac{m}{x}$(m≠0)位于第二象限的一支于C点,OA=OB=2.
如图,一条直线分别交x轴、y轴于A、B两点,交反比例函数y=$\frac{m}{x}$(m≠0)位于第二象限的一支于C点,OA=OB=2.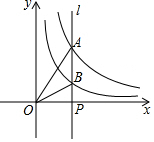 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{5}{x}$(x>0)及y2=$\frac{k}{x}$(x>0)的图象分别交于A、B,若△AOB的面积为2,则k=1.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{5}{x}$(x>0)及y2=$\frac{k}{x}$(x>0)的图象分别交于A、B,若△AOB的面积为2,则k=1.
 如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为80°.
如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为80°.