题目内容
6．
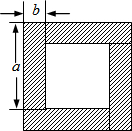如图所示的是用四块完全相同的小长方形拼成的一个“回形”正方形．（1）用两个不同的代数式表示图中的阴影部分的面积，你能得到怎样的等式？
（2）利用（1）中的结论计算：已知（a+b）2=4，ab=$\frac{3}{4}$，求（a-b）2．
分析 （1）根据阴影部分的面积=4个小长方形的面积=大正方形的面积-小正方形的面积，利用完全平方公式，即可解答；
（2）根据完全平方公式解答．
解答 解：（1）阴影部分的面积为：4ab或（a+b）2-（a-b）2，
得到等式：4ab=（a+b）2-（a-b）2，
说明：（a+b）2-（a-b）2=a2+2ab+b2-（a2-2ab+b2）=a2+2ab+b2-a2+2ab-b2=4ab．
（2）（a-b）2=（a+b）2-4ab=4-4×$\frac{3}{4}$=4-3=1，
∴a-b=±1．
点评 本题考查了完全平方公式的几何背景，准确识图，根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
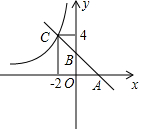如图，一条直线分别交x轴、y轴于A、B两点，交反比例函数y=$\frac{m}{x}$（m≠0）位于第二象限的一支于C点，OA=OB=2．
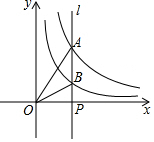如图，直线l⊥x轴于点P，且与反比例函数y1=$\frac{5}{x}$（x＞0）及y2=$\frac{k}{x}$（x＞0）的图象分别交于A、B，若△AOB的面积为2，则k=1．
16．下列分式运算，正确的是（ ）
| A． | ${（\frac{2b}{3a}）^2}=\frac{{2{b^2}}}{{3{a^2}}}$ | B． | $\frac{{{x^2}-4}}{x-2}=x-2$ | C． | $2x•\frac{1}{2x}=\frac{1}{{4{x^2}}}$ | D． | $\frac{1}{x-y}+\frac{1}{y-x}=0$ |