题目内容
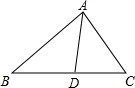
如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是__________.

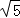 .
.
【考点】轴对称-最短路线问题.
【专题】压轴题;动点型.
【分析】首先确定DC′=DE+EC′=DE+CE的值最小.然后根据勾股定理计算.
【解答】解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于E,连接CE,
此时DE+CE=DE+EC′=DC′的值最小.
连接BC′,由对称性可知∠C′BE=∠CBE=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=2,
∵D是BC边的中点,
∴BD=1,
根据勾股定理可得DC′=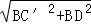 =
=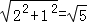 .
.
故答案为: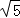 .
.
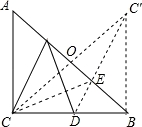
【点评】此题考查了线路最短的问题,确定动点E何位置时,使EC+ED的值最小是关键.

练习册系列答案
相关题目