Question

△ABC中，点O是△ABC内一点且到△ABC三边的距离相等，∠A=40°，则∠BOC=__________．

Answer 1

110°．

【考点】角平分线的性质．

【分析】根据O到三角形三边距离相等，得到O是内心，再利用三角形内角和定理和角平分线的概念即可求出∠BOC的度数．

【解答】解：∵O到三角形三边距离相等，

∴O是内心，

∴AO，BO，CO都是角平分线，

∴∠CBO=∠ABO=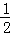∠ABC，∠BCO=∠ACO=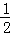∠ACB，

∠ABC+∠ACB=180°﹣40°=140°，

∠OBC+∠OCB=70°，

∠BOC=180°﹣70°=110°．

故答案为：110°．

【点评】本题考查的是角平分线的定义和三角形的内心的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．