题目内容
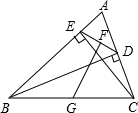
如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.
【考点】直角三角形斜边上的中线;等腰三角形的判定与性质.
【专题】证明题.
【分析】连接EG、FG,根据直角三角形斜边上的中线等于斜边的一半可得DG=EG= BC,再根据等腰三角形三线合一的证明即可.
BC,再根据等腰三角形三线合一的证明即可.
【解答】证明:如图,

连接GE、GD,
∵△ABC中,BD、CE是高,
∴△BEC和△BDC是直 角三角形,
角三角形,
∵G是BC的中点,
∴GE=GD= BC,
BC,
∴△GED是等腰三角形,
∵F是DE的中点,
∴GF⊥DE.
【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并作出辅助线构造出等腰三角形是解题的关键.

练习册系列答案
相关题目