题目内容
 如图,在平面直角坐标系中,菱形ABCD的顶点B、C的坐标分别为B(0,0),C(6,0),且∠B=60°.动点P、Q分别从点B、点D同时出发,点P以每秒2个单位的速度向点A移动;点Q以每秒3个单位的速度向点A移动.设两动点运动的时间为t秒,其中0<t<2.
如图,在平面直角坐标系中,菱形ABCD的顶点B、C的坐标分别为B(0,0),C(6,0),且∠B=60°.动点P、Q分别从点B、点D同时出发,点P以每秒2个单位的速度向点A移动;点Q以每秒3个单位的速度向点A移动.设两动点运动的时间为t秒,其中0<t<2.(1)当t=
(2)记△POC的面积为S1;△APQ的面积为S2.试探求S1+S2有没有最小值?若有,求出最小值及此时点P的坐标;若没有,说明理由;
(3)是否存在t值,使PQ⊥AC?说明理由.
考点:四边形综合题
专题:
分析:(1)根据菱形的性质证得△OCP≌△ACQ,从而得到PO=QA,根据点P以每秒2个单位的速度向点A移动;点Q以每秒3个单位的速度向点A移动,表示出PO=2t,AQ=6-3t,从而列出方程2t=6-3t求解;
(2)过点P作EF平行于y轴,分别交BC、AD于点E、F,分别表示出BP=2t,AQ=6-3t,得到PE=
t,PF=
(3-t),然后分别表示出S1=3
t和S2=
(2-t)(3-t),从而得到S1+S2=3
t+
(2-t)(3-t)确定最小值及点P的坐标;
(3)根据菱形的性质得AC平分∠BAD,根据若有AP=AQ,可得PQ⊥AC,但AP=6-2t,DQ=6-3t,AP≠DQ,从而的不存在t值,使PQ⊥AC.
(2)过点P作EF平行于y轴,分别交BC、AD于点E、F,分别表示出BP=2t,AQ=6-3t,得到PE=
| 3 |
| 3 |
| 3 |
3
| ||
| 2 |
| 3 |
3
| ||
| 2 |
(3)根据菱形的性质得AC平分∠BAD,根据若有AP=AQ,可得PQ⊥AC,但AP=6-2t,DQ=6-3t,AP≠DQ,从而的不存在t值,使PQ⊥AC.
解答: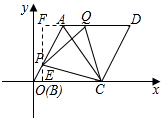 解:(1)∵菱形ABCD中,∠B=60°,
解:(1)∵菱形ABCD中,∠B=60°,
∴∠DCA=∠ACO=60°,
∴OC=AC,
当△PCQ是等边三角形时,CP=CP,∠QCP=60°,
∴∠QCA=∠PCB,
在△OCP和△ACQ中,
∴△OCP≌△ACQ(SAS),
∴PO=QA,
∵点P以每秒2个单位的速度向点A移动;点Q以每秒3个单位的速度向点A移动,
∴PO=2t,AQ=6-3t,
∴2t=6-3t,
解得:t=
;
(2)过点P作EF平行于y轴,分别交BC、AD于点E、F,
根据题意得:BP=2t,AQ=6-3t,
∴PE=
t,PF=
(3-t),
∴S1=3
t,S2=
(2-t)(3-t),
∴S1+S2=3
t+
(2-t)(3-t)=
(t-
)2+
,
∴S1+S2有最小值,且最小值为
,
∴此时点P的坐标为(
,
);
(3)∵四边形ABCD是菱形,
∴AC平分∠BAD,
若有AP=AQ,可得PQ⊥AC,
但AP=6-2t,AQ=6-3t,AP≠DQ,
∴不存在t值,使PQ⊥AC.
 解:(1)∵菱形ABCD中,∠B=60°,
解:(1)∵菱形ABCD中,∠B=60°,∴∠DCA=∠ACO=60°,
∴OC=AC,
当△PCQ是等边三角形时,CP=CP,∠QCP=60°,
∴∠QCA=∠PCB,
在△OCP和△ACQ中,
|
∴△OCP≌△ACQ(SAS),
∴PO=QA,
∵点P以每秒2个单位的速度向点A移动;点Q以每秒3个单位的速度向点A移动,
∴PO=2t,AQ=6-3t,
∴2t=6-3t,
解得:t=
| 6 |
| 5 |
(2)过点P作EF平行于y轴,分别交BC、AD于点E、F,
根据题意得:BP=2t,AQ=6-3t,
∴PE=
| 3 |
| 3 |
∴S1=3
| 3 |
3
| ||
| 2 |
∴S1+S2=3
| 3 |
3
| ||
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
45
| ||
| 8 |
∴S1+S2有最小值,且最小值为
45
| ||
| 8 |
∴此时点P的坐标为(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
(3)∵四边形ABCD是菱形,
∴AC平分∠BAD,
若有AP=AQ,可得PQ⊥AC,
但AP=6-2t,AQ=6-3t,AP≠DQ,
∴不存在t值,使PQ⊥AC.
点评:本题考查了四边形的综合知识,题目中涉及的动点问题更是中考的热点考点之一,应加强训练,难度偏大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
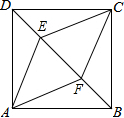 如图,正方形ABCD中,点E、F为对角线BD上两点,DE=BF.
如图,正方形ABCD中,点E、F为对角线BD上两点,DE=BF. 已知:正比例函数y=ax的图象与反比例函数y=
已知:正比例函数y=ax的图象与反比例函数y= 解不等式组
解不等式组