题目内容
8. 如图1,若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD•DC等于( )
如图1,若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD•DC等于( )| A. | 3 | B. | 6 | C. | 7 | D. | 12 |
分析 延长BP到E使PE=PB=4,连结AE,如图,则PE=PA,根据等腰三角形的性质和三角形外角性质可判断∠APB=2∠E,由于∠APB=2∠ACB,则∠E=∠C,于是可证明△ADE∽△BDC,然后利用相似比可计算出AD•CD的值.
解答 解:延长BP到E使PE=PB=4,连结AE,如图,
∵PA=PB,
∴PE=PA,
∴∠1=∠E,
而∠APB=∠1+∠E,
∴∠APB=2∠E,
∵∠APB=2∠ACB,
∴∠E=∠C,
而∠ADE=∠CDB,
∴△ADE∽△BDC,
∴$\frac{AD}{BD}$=$\frac{ED}{CD}$,
∴AD•CD=BE•ED=(4+3)•(4-3)=7.
故选C.
点评 本题考查了相似三角形的判定与性质:两个三角形相似也有对应角相等,对应边的比相等.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.解决本题的关键是构建△ADE与△BDC相似.

练习册系列答案
相关题目
20.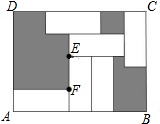 如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )
如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )
 如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )
如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )| A. | 105 | B. | 106 | C. | 107 | D. | 108 |
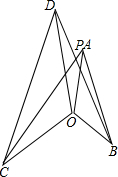 如图,△AOB与△COD中,OA=OB,OC=OD,∠AOB=∠COD,AC与BD交于点P.
如图,△AOB与△COD中,OA=OB,OC=OD,∠AOB=∠COD,AC与BD交于点P.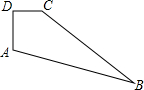 如图,在四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,则四边形ABCD的面积为144.
如图,在四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,则四边形ABCD的面积为144.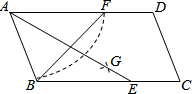 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )