题目内容
18.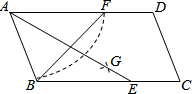 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )| A. | 16 | B. | 15 | C. | 14 | D. | 13 |
分析 首先证明四边形ABEF是菱形,得出AE⊥BF,OB=OF=6,OA=OE,利用勾股定理计算出AO,从而得到AE的长.
解答 解:连结EF,AE与BF交于点O,如图,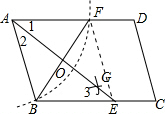
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴AE=2OA=16.
故选:A.
点评 本题考查了平行四边形的性质、菱形的判定与性质、等腰三角形的判定、勾股定理;熟练掌握平行四边形的性质,证明四边形ABEF为菱形是解决问题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
9.下列调查中,适合采用全面调查的是( )
| A. | 对全国中学生心理健康现状的调查 | B. | 对某种食品合格情况的调查 | ||
| C. | 对某电视节目收视率的调查 | D. | 对你所在班级同学身高情况的调查 |
7.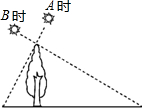 如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )
如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )
 如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )
如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )| A. | 2m | B. | $\sqrt{3}$m | C. | $\sqrt{2}$m | D. | $\sqrt{5}$m |
 如图1,若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD•DC等于( )
如图1,若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD•DC等于( )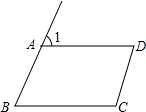 如图,∠B=∠1,那么根据两直线平行,同位角相等,可得AD∥BC.
如图,∠B=∠1,那么根据两直线平行,同位角相等,可得AD∥BC.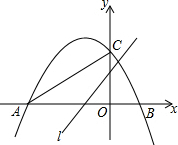 如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=$\sqrt{3}$x+m从点C开始沿y轴向下平移.
如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=$\sqrt{3}$x+m从点C开始沿y轴向下平移.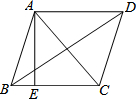 已知菱形ABCD的两条对角线AC,BD长分别为6cm、8cm,且AE⊥BC,这个菱形的面积S=24cm2,AE=$\frac{24}{5}$cm.
已知菱形ABCD的两条对角线AC,BD长分别为6cm、8cm,且AE⊥BC,这个菱形的面积S=24cm2,AE=$\frac{24}{5}$cm.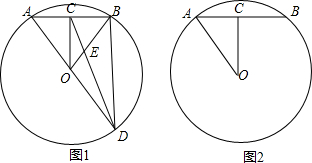
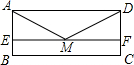 如图,矩形ABCD,E、F在AB、CD上,且EF∥AD,M为EF的中点,连接AM、DM,求证:AM=DM.
如图,矩形ABCD,E、F在AB、CD上,且EF∥AD,M为EF的中点,连接AM、DM,求证:AM=DM.