题目内容
15.在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是y=-x2+4(0<x<2).分析 根据剩下部分的面积=大正方形的面积-小正方形的面积得出y与x的函数关系式即可.
解答 解:设剩下部分的面积为y,则:
y=-x2+4(0<x<2),
故答案为:y=-x2+4(0<x<2).
点评 此题主要考查了根据实际问题列二次函数关系式,利用剩下部分的面积=大正方形的面积-小正方形的面积得出是解题关键.

练习册系列答案
相关题目
10.如果抛物线A:y=x2-1通过左右平移得到抛物线B,再通过上下平移抛物线B得到抛物线C:y=x2-2x+2,那么抛物线B的表达式为( )
| A. | y=x2+2 | B. | y=x2-2x-1 | C. | y=x2-2x | D. | y=x2-2x+1 |
4.已知一个坡的坡比为i,坡角为α,则下列等式成立的是( )
| A. | i=sinα | B. | i=cosα | C. | i=tanα | D. | i=cotα |
5.定义运算$\frac{a}{b}$=$\frac{a+1}{b+1}$,若a≠-1,b≠-1,则下列等式中不正确的是( )
| A. | $\frac{a}{b}$×$\frac{b}{a}$=1 | B. | $\frac{b}{a}$+$\frac{c}{a}$=$\frac{b+c}{a}$ | ||
| C. | ($\frac{a}{b}$)2=$\frac{({a}^{2}+2a)}{({b}^{2}+2b)}$ | D. | $\frac{a}{a}$=1 |
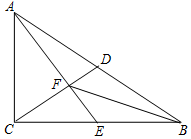 如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CE•CB.
如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CE•CB.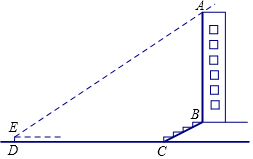 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) 如图,在△ABC中,AC=4,D为BC上一点,CD=2,且△ADC与△ABD的面积比为1:3;
如图,在△ABC中,AC=4,D为BC上一点,CD=2,且△ADC与△ABD的面积比为1:3;