��Ŀ����
8���������С��ͬ�ĺ�30��ǵ�ֱ�����ǰ壨��BAC=��B1A1C=30�㣩��ͼ1�ķ�ʽ���ã��̶����ǰ�A1B1C��Ȼ�����ǰ�ABC��ֱ�߶���C˳ʱ�뷽����ת����ת��С��90�㣩��ͼ2��ʾ��λ�ã�AB��A1C��A1B1���ڵ�D��E��AC��A1B1���ڵ�F����1����֤��BD=B1F��
��2������ת�ǵ���30��ʱ��AB��A1B1��ֱ�𣿲�˵�����ɣ�
��3������ͼ1ֱ���ж����⡰ֱ����������30������Եıߵ���б�ߵ�һ�롱����������⣨�������������⣩����ͼ2�����ǰ�ABC�Ƶ�C˳ʱ����ת��ͼ3��λ�ã���AB��CB1ʱ����ֱ��д��A1D��CD��������ϵ��A1D=CD

���� ��1�����жϳ���A1CB=��ACB1�������жϳ���BCD�ա�B1CF�����ɵó����ۣ�
��2�����жϳ���AFE=��ACB1=60�㣬���������AEF=90�㣬���ɵó����ۣ�
��3�����жϳ���ABB1�ǵȱ������μ��ɵó����ۣ�
�������ACD=60�㣬�����жϳ���ACD��ֱ�������μ��ɵó����ۣ�
��� �⣺��1��������֪��BC=BC1����B=��B1����ACB=��A1CB1=90�㣬
����ת֪����A1CB=��ACB1��
�ڡ�BCD�͡�B1CF�У�$\left\{\begin{array}{l}{��B=��{B}_{1}}\\{BC={B}_{1}C}\\{��BCD=��{B}_{1}CF}\end{array}\right.$��
���BCD�ա�B1CF��
��BD=B1F��
��2��AB��A1B1��ֱ��
���ɣ�����ת��Ϊ30�㣬
���ACA1=30�㣬
���B1CF=90��-30��=60�㣬
�ߡ�B1=60�㣬
���B1FC=180��-��B1-��ACB1=60�㣬
���AFE=60�㣬
�ߡ�A=30�㣬
���AEF=180��-��A-��AFE=90�㣬
��AB��A1B1��
��3��������֪����BAC=��B1AC=30�㣬��B=��B1��
���ABA1�ǵȱ������Σ�
��BB1=AB��
��BB1=BC+B1C=2BC��
��BC=$\frac{1}{2}$AB��
��ֱ����������30������Եıߵ���б�ߵ�һ�룬
�ʴ�Ϊ�������⣻
��AB��CB1��
���ACB1=��A=30�㣬
���ACD=90��-30��=60�㣬
���ADC=180��-��A-��ACD=90�㣬
��Rt��ACD�У���A=30�㣬
��CD=$\frac{1}{2}$AC��ֱ����������30������Եıߵ���б�ߵ�һ�룩��
��AC=A1C��
��CD=$\frac{1}{2}$A1C��
��A1D+CD=A1C��
��A1D=CD��
�ʴ�Ϊ��A1D=CD��
���� �����Ǽ��α任�ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ������ε��ڽǺͶ������ȱ������ε��ж������ʣ��⣨1���Ĺؼ����жϳ���A1CB=��ACB1���⣨2���Ĺؼ��������AFE=60�㣬�⣨3���Ĺؼ����жϳ���ABB1�ǵȱ������Σ���һ���е��Ѷȵ��п������⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д�| A�� | 5 | B�� | 6 | C�� | $\sqrt{7}$ | D�� | 5��$\sqrt{7}$ |
| A�� | �ۼƹ��ﲻ����50Ԫ | |
| B�� | �ۼƹ��ﳬ��50Ԫ��������100Ԫ | |
| C�� | �ۼƹ��ﳬ��100Ԫ | |
| D�� | �ۼƹ��ﲻ����50Ԫ��պ�Ϊ150Ԫ |
| A�� | 15�� | B�� | 30�� | C�� | 30���60�� | D�� | 30���150�� |
 ��ij�е�·��ͨ�����������涨��С�����ڳ��н�·����ʻ�ٶȲ��ó���60ǧ��/Сʱ����ͼ��һ��С������һ�����н�·��ֱ����ʻ��ijһʱ�̸պ���ʻ��·��Գ��ټ����A��ǰ��30��C��������2���B�������С�����복�ټ���Ǽ����Ϊ50�ף���������С������������Ϊʲô�������٣������˶��٣�
��ij�е�·��ͨ�����������涨��С�����ڳ��н�·����ʻ�ٶȲ��ó���60ǧ��/Сʱ����ͼ��һ��С������һ�����н�·��ֱ����ʻ��ijһʱ�̸պ���ʻ��·��Գ��ټ����A��ǰ��30��C��������2���B�������С�����복�ټ���Ǽ����Ϊ50�ף���������С������������Ϊʲô�������٣������˶��٣�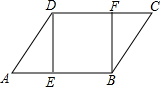 ��ͼ����?ABCD�У�E��F�ֱ���AB��DC���ϵĵ㣬��AE=CF��
��ͼ����?ABCD�У�E��F�ֱ���AB��DC���ϵĵ㣬��AE=CF��