题目内容
惠民超市第一天以每件10元的价格购进某品牌茶杯15个,由于此种品牌商品价格看涨,第二天又以每件12元的价格购进同种茶杯35个,然后以相同的价格卖出,商店在销售这些茶杯时,要想利润率不低于10%,你觉得该如何定价?
考点:一元一次方程的应用
专题:
分析:可设每个茶杯的最低售价为x元,根据等量关系:利润率最低为10%,列出方程求解即可.
解答:解:设每个茶杯的最低售价为x元,由题意,得
15(x-10)+35(x-12)=(15×10+35×12)×10%,
解得x=12.54.
答:商店在销售这些茶杯时每个茶杯的售价不能低于12.54元.
15(x-10)+35(x-12)=(15×10+35×12)×10%,
解得x=12.54.
答:商店在销售这些茶杯时每个茶杯的售价不能低于12.54元.
点评:考查了一元一次方程销售问题的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
关于直线、射线和线段的描述正确的是( )
| A、直线、射线和线段的长度都不确定 |
| B、射线是直线长度的一半 |
| C、直线最长,线段最短 |
| D、直线没有端点,射线有一个端点,线段有两个端点 |
下列结论错误的是( )
| A、若ac=bc,则a=b |
| B、若a+c=b+c,则a=b |
| C、若a=b,则a+c=b+c |
| D、若a=b,则ac=bc |
下列计算结果为负数是( )
| A、(-2)-(-3) |
| B、3+|-5| |
| C、(-2)×(-5) |
| D、(-2)3 |
 如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是
如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是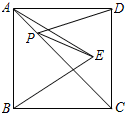 如图所示,正方形ABCD内作△ABE是等边三角形,在对角线AC上有一点P,使PD+PE的和最小为5,则这个正方形ABCD的面积为
如图所示,正方形ABCD内作△ABE是等边三角形,在对角线AC上有一点P,使PD+PE的和最小为5,则这个正方形ABCD的面积为 已知抛物线y=x2-2x+3经过点B(3,6),与y轴交于点A(0,3),若点M是直线AB:y=x+3下方抛物线上的一点,且S△ABM=3,求点M的坐标.
已知抛物线y=x2-2x+3经过点B(3,6),与y轴交于点A(0,3),若点M是直线AB:y=x+3下方抛物线上的一点,且S△ABM=3,求点M的坐标. 2014年5月31日是世界卫生组织发起的第27个“世界无烟日”.为了更好地宣传吸烟的危害,某中学九年级(1)班数学兴趣小组设计了如下调查问卷,在东方广场随机调查了部分吸烟人群,并将调查结果绘制成如图所示的统计图.
2014年5月31日是世界卫生组织发起的第27个“世界无烟日”.为了更好地宣传吸烟的危害,某中学九年级(1)班数学兴趣小组设计了如下调查问卷,在东方广场随机调查了部分吸烟人群,并将调查结果绘制成如图所示的统计图.