题目内容
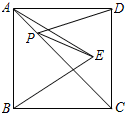如图所示，正方形ABCD内作△ABE是等边三角形，在对角线AC上有一点P，使PD+PE的和最小为5，则这个正方形ABCD的面积为考点：轴对称-最短路线问题
专题：
分析：根据正方形的性质可得点B、D关于AC对称，再根据轴对称确定最短路线问题判断出BE的值为PD+PE的和最小值，然后根据等边三角形的三条边都相等可得AB=BE，再根据正方形的面积公式列式计算即可得解．
解答：解：∵四边形ABCD是正方形，
∴点B、D关于AC对称，
∴BE的值为PD+PE的和最小值，
∴BE=5，
∵△ABE是等边三角形，
∴AB=BE=5，
∴正方形ABCD的面积=52=25．
故答案为：25．
∴点B、D关于AC对称，
∴BE的值为PD+PE的和最小值，
∴BE=5，
∵△ABE是等边三角形，
∴AB=BE=5，
∴正方形ABCD的面积=52=25．
故答案为：25．
点评：本题考查了轴对称确定最短路线问题，正方形的性质，等边三角形的性质，判断出BE的长度为PD+PE的最小值是解题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
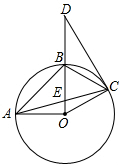如图，已知⊙O上A、B、C三点，∠BAC=∠BCD，D是OB延长线上的点，∠BDC=30°，⊙O半径为2，AO⊥BO，BO与AC交于点E．
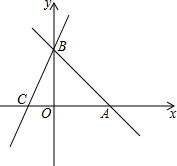直线AB：y=-x-b分别与x，y轴交于A（6，0）、B两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．
在△ABC中，∠ACB=∠ABC，如果这个三角形的一个外角为110°，求∠ACB的度数．