题目内容
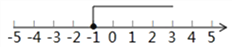
定义一种新的运算：a※b=2a+b，已知关于x不等式x※k≥-1的解集在数轴上表示如图，则k= __________
1
【解析】根据新定义，可知x※k=2x+k≥-1，解得x≥，根据数轴可知x≥-1，可知=-1，解得k=1.
练习册系列答案
相关题目
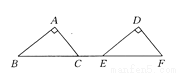
如图所示，△ABC经过平移得到△DEF，已知CE＝2 cm，AC＝3 cm，AB＝4 cm，∠A＝90°，则CF＝_________cm，平移的距离是_________．
7 7 cm
【解析】试题分析：在Rt△ABC中，由勾股定理得：
BC＝＝＝5（cm），
∵△ABC经过平移得到△DEF，
∴EF＝BC＝5cm，
∴CF＝CE＋EF＝2＋5＝7（cm），
∵C点与F点对应，
∴平移的距离是CF的长度，
即平移的距离是7cm．
故答案为：7，7cm． 连续平移只改变图形的那方面，没有改变图形的哪几方面？
连续平移只改变图形的位置，没有改变图形的形状、大小.
【解析】试题分析：根据平移的特征回答即可.
试题解析：
根据平移的特征可以得出连续平移只改变图形的位置，没有改变图形的 形状、大小. 下列说法正确的是( )
A. 平移改变图形的形状
B. 平移改变图形的大小
C. 平移改变物体的形状和大小
D. 平移不改变物体的形状和大小
D
【解析】试题解析：平移的特点是不变形，即平移不改变物体的形状和大小.
故选D. 将长度为5cm的线段向上平移10cm所得线段长度是（ ）
A. 10cm B. 5cm C. 0cm D. 无法确定
B
【解析】平移不改变图形的大小和形状．故线段长度不变，仍为5cm． 下列说法正确的有（ ）
①4是x﹣3＞1的解；②不等式x﹣2＜0的解有无数个；③x＞5是不等式x+2＞3的解集；④x=3是不等式x+2＞1的解；⑤不等式x+2＜5有无数个正整数解．
A．1个 B．2个 C．3个 D．4个
B.
【解析】
试题分析：解x﹣3＞1得：x＞4，所以4不是x﹣3＞1的解，故①错误；不等式x﹣2＜0的解有无数个，此说法正确，故②正确；解不等式x+2＞3得：x＞1，所以x＞5不是不等式x+2＞3的解集，故③错误；解不等式x+2＞1得：x＞-1,所以x=3是不等式x+2＞1的解，故④正确；解不等式x+2＜5得：x＜3,所以其正整数解为1，2共2个.故⑤错误.
故选B. 已知x=2是不等式（x-5）（ax-3a+2）≤0的解，且x=1不是这个不等式的解，则实数a的取值范围是（ ）
A. a＞1 B. a≤2 C. 1＜a≤2 D. 1≤a≤2
C
【解析】根据x=2是不等式（x-5）（ax-3a+2）≤0的解，可知（2-5）（2a-3a+2）≤0，解得：a≤2，再根据x=1不是这个不等式的解，可得（1-5）（a-3a+2）＞0，解得：a＞1，
由此可得a的取值范围为：1＜a≤2．
故选：C. 用反证法证明“三角形中至少有一个内角不小于60°”，应先假设这个三角形中（ ）
A. 有一个内角小于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 每一个内角都大于60°
B
【解析】试题分析：此题要运用反证法，由题意先假设三角形的三个角都小于60°成立．然后推出不成立．得出选项．
【解析】
设三角形的三个角分别为：a，b，c．
假设，a＜60°，b＜60°，c＜60°，
则a+b+c＜60°+60°+60°，
即，a+b+c＜180°与三角形内角和定理a+b+c=180°矛盾．
所以假设不成立，即三角形中至少有一个角不小于60... 将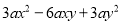
分解因式是___________
【解析】根据题意，先提公因式，再根据平方差公式分解即可得： .
故答案为： .