题目内容

18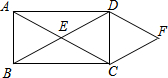．已知：如图，在矩形ABCD中，对角线BD与AC相交于点E，DF∥AC，CF∥BD，直线DF与CF相交于点F．求证：四边形EDFC是菱形．

分析 先证明四边形DECF是平行四边形，由矩形的性质得出DE=EC，即可得出四边形DECF是菱形．

解答 证明：∵DF∥AC，CF∥BD，
∴四边形DECF是平行四边形，
∵四边形ABCD是矩形，
∴BD=AC，DE=$\frac{1}{2}BD$，$EC=\frac{1}{2}AC$，
∴DE=EC，
∵四边形DECF是平行四边形，
∴四边形DECF是菱形．

点评 本题考查了菱形的判定、矩形的性质、平行四边形的判定；熟练掌握矩形的性质是解决问题的关键．

练习册系列答案
相关题目
8．已知关于x的一元二次方程x2-2x-t+1=0有两个实数根．
（1）求t的取值范围；
（2）设v是方程的一个实数根，且满足（v2-2v+3）（t-3）=-5，求t的值．
9．在数轴上表示不等式3x+1≥4的解集，正确的是（　　）
A．B．C．D．
6．下列命题不正确的是（　　）
A．平行四边形对角相等B．矩形的对角线相等
C．两直线平行，同位角相等D．平分弦的直径垂直于这条弦
13．解方程
（1）$\frac{2}{x-3}$=$\frac{3}{2x-1}$                      
（2）$\frac{x-2}{x+2}$=$\frac{x+2}{x-2}$+$\frac{16}{{x}^{2}-4}$
（3）$\frac{2{x}^{2}}{2{x}^{2}-x-1}$+$\frac{3}{1-x}$=1          
（4）$\frac{2x+4}{{x}^{2}+2x}$=$\frac{1}{x+2}$+$\frac{2}{x}$．
3．下列命题是假命题的是（　　）
A．邻补角一定互补
B．不重合的两条直线只有两种位置关系：相交和平行
C．对顶角相等
D．垂线段最短
10．一种计算机每秒可运算4×108次，它工作3×103秒运算的次数用科学记数法表示为1.2×1012（次）．
7．下列多项式的乘法中可用平方差公式计算的是（　　）
A．（1+x）（x+1）B．（2a+b）（b-2a）C．（-a+b）（a-b）D．（x2-y）（y2+x）
8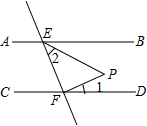．如图，直线AB∥CD，直线EF分别于AB，CD交于点E，F，FP⊥EF于点F，且与∠BEF的平分线交于点P，若∠1=20°，则∠2的度数是（　　）
A．35°B．30°C．25°D．20°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网