��Ŀ����
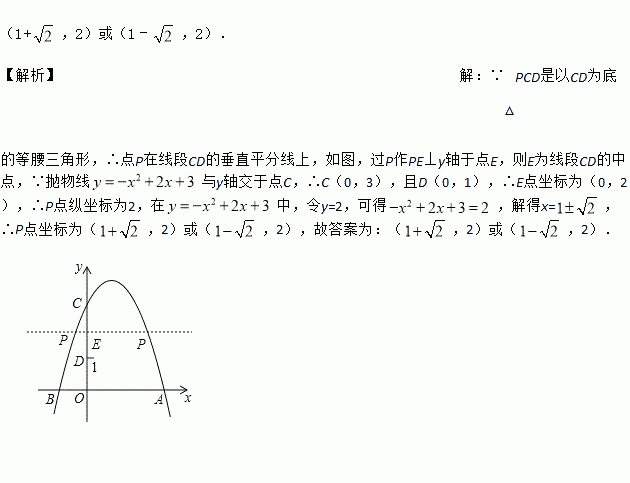
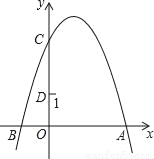
��ͼ��������y=��x2+2x+3��y�ύ�ڵ�C����D��0��1������P���������ϵĶ��㣮����PCD����CDΪ�ĵ��������Σ����P������Ϊ�� ����
 ��1+��2����1����2����
����������������
�ߡ�PCD����CDΪ�ĵ��������Σ����P���߶�CD�Ĵ�ֱƽ�����ϣ���ͼ����P��PE��y���ڵ�E����EΪ�߶�CD���е㣬����������y�ύ�ڵ�C����C��0��3������D��0��1������E������Ϊ��0��2������P��������Ϊ2�����У���y=2���ɵã����x=����P������Ϊ����2����2�����ʴ�Ϊ������2����2����
��1+��2����1����2����
����������������
�ߡ�PCD����CDΪ�ĵ��������Σ����P���߶�CD�Ĵ�ֱƽ�����ϣ���ͼ����P��PE��y���ڵ�E����EΪ�߶�CD���е㣬����������y�ύ�ڵ�C����C��0��3������D��0��1������E������Ϊ��0��2������P��������Ϊ2�����У���y=2���ɵã����x=����P������Ϊ����2����2�����ʴ�Ϊ������2����2����
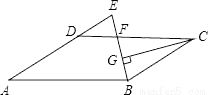
��ͼ����?ABCD�У�AB=12��AD=8����ABC��ƽ���߽�CD�ڵ�F����AD���ӳ����ڵ�E��CG��BE������ΪG����EF=2�����߶�CG�ij�Ϊ��������
A. 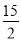 B.
B. 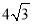 C.
C. 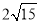 D.
D. 
 C
���������ߡ�ABC��ƽ���߽�CD�ڵ�F��
���ABE=��CBE��
���ı���ABCD��ƽ���ı��Σ�
��DC��AB��
���CBE=��CFB=��ABE=��E��
��CF=BC=AD=8��AE=AB=12��
��AD=8��
��DE=4��
��DC��AB��
�࣬
�࣬
��EB=6��
��CF=CB��CG��BF��
��BG=BF=2...
C
���������ߡ�ABC��ƽ���߽�CD�ڵ�F��
���ABE=��CBE��
���ı���ABCD��ƽ���ı��Σ�
��DC��AB��
���CBE=��CFB=��ABE=��E��
��CF=BC=AD=8��AE=AB=12��
��AD=8��
��DE=4��
��DC��AB��
�࣬
�࣬
��EB=6��
��CF=CB��CG��BF��
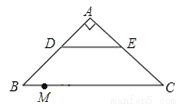
��BG=BF=2... ��2016����ʡ�����У���ͼ����Rt��ABC�У���A=90�㣬AB=AC��BC=20��DE�ǡ�ABC����λ�ߣ���M�DZ�BC��һ�㣬BM=3����N���߶�MC�ϵ�һ�����㣬����DN��ME��DN��ME�ཻ�ڵ�O������OMN��ֱ�������Σ���DO�ij���______��
 ��
����������ͼ��֪���ڡ�OMN�У���OMN�Ķ�����һ����ֵ���ҡ�OMN��Ϊֱ��. �ʵ���ONM=90����MON=90��ʱ����OMN��ֱ��������. ��ˣ�������Ҫ��������������ֱ����.
(1) ����ONM=90��ʱ����DN��BC.
����E��EF��BC������ΪF.(��ͼ)
����Rt��ABC�У���A=90�㣬AB=AC��
���C=45�㣬
��BC=20��
...
��
����������ͼ��֪���ڡ�OMN�У���OMN�Ķ�����һ����ֵ���ҡ�OMN��Ϊֱ��. �ʵ���ONM=90����MON=90��ʱ����OMN��ֱ��������. ��ˣ�������Ҫ��������������ֱ����.
(1) ����ONM=90��ʱ����DN��BC.
����E��EF��BC������ΪF.(��ͼ)
����Rt��ABC�У���A=90�㣬AB=AC��
���C=45�㣬
��BC=20��
... ����˵��������ǣ�������
A. �Խ�����ƽ�ֵ��ı�����ƽ���ı���
B. ����Ա߷ֱ���ȵ��ı�����ƽ���ı���
C. һ��Ա�ƽ������ȵ��ı�����ƽ���ı���
D. һ��Ա���ȣ���һ��Ա�ƽ�е��ı�����ƽ���ı���
 D
��������һ��Ա���ȣ���һ��Ա�ƽ�в����ж��ı���Ϊƽ���ı��Σ���Dѡ�����.
��ѡD.
D
��������һ��Ա���ȣ���һ��Ա�ƽ�в����ж��ı���Ϊƽ���ı��Σ���Dѡ�����.
��ѡD. ��ƽ��ֱ������ϵxOy�У�������y=ax2+bx+2��B����2��6����C��2��2�����㣮
��1���������߶���ΪD�����BCD�������
��2����ֱ��y=�� x����ƽ��b����λ���õ�ֱ���������߶�BDC�������˵�B��C���������������㣬��b��ȡֵ��Χ��
x����ƽ��b����λ���õ�ֱ���������߶�BDC�������˵�B��C���������������㣬��b��ȡֵ��Χ��
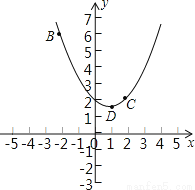
 ��1��3 ��2����b��3��
����������1�����ݴ���ϵ�������ɽ�����⣮���ֱ��BC��Գ���Ľ���H������S��BDC=S��BDH+S��DHC���ɽ�����⣮
��2���ɣ���������ֻ��һ���ʱ���b��ֵ����ֱ��y=��x+b������Cʱ�����b��ֵ����ֱ��y=��x+b������Bʱ�����b��ֵ���ɴ˼��ɽ�����⣮
��������
��1���������ã�
�������߽���ʽΪy=x2��x+2��
��...
��1��3 ��2����b��3��
����������1�����ݴ���ϵ�������ɽ�����⣮���ֱ��BC��Գ���Ľ���H������S��BDC=S��BDH+S��DHC���ɽ�����⣮
��2���ɣ���������ֻ��һ���ʱ���b��ֵ����ֱ��y=��x+b������Cʱ�����b��ֵ����ֱ��y=��x+b������Bʱ�����b��ֵ���ɴ˼��ɽ�����⣮
��������
��1���������ã�
�������߽���ʽΪy=x2��x+2��
��... ��֪���κ���y=ax2+bx��1��a��0����ͼ���㣨1��1���������ʽ1��a��b��ֵΪ��������
A. ��1 B. 2 C. ��3 D. 5
 A
����������������
�߶��κ���y=ax2+bx��1��a��0����ͼ���㣨1��1������a+b��1=1����1��a��b=��1��
��ѡA��
A
����������������
�߶��κ���y=ax2+bx��1��a��0����ͼ���㣨1��1������a+b��1=1����1��a��b=��1��
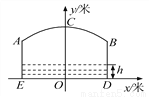
��ѡA�� ��ͼ��С������һ���ţ����ż��ӵ��Ľ����������������ߵ�һ����ACB�;��ε�����AE��ED��DB��ɣ���֪�ӵ�ED��ˮƽ�ģ�ED��16m��AE��8m�������ߵĶ���C��ED�ľ�����11m����ED���ڵ�ֱ��Ϊx�ᣬ�����ߵĶԳ���Ϊy�Ὠ��ƽ��ֱ������ϵ��
(1)�������ߵĽ���ʽ��
(2)��֪��ijʱ�̿�ʼ��40h�ڣ�ˮ����ӵ�ED�ľ���h(��λ��m)��ʱ��t(��λ��h)�ı仯���㺯����ϵh����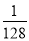 (t��19)2��8(0��t��40)�ҵ�ˮ�浽����C�ľ��벻����5mʱ�����ֹ��ֻͨ�У���ͨ������˵��������һʱ���ڣ������Сʱ��ֹ��ֻͨ�У�
(t��19)2��8(0��t��40)�ҵ�ˮ�浽����C�ľ��벻����5mʱ�����ֹ��ֻͨ�У���ͨ������˵��������һʱ���ڣ������Сʱ��ֹ��ֻͨ�У�
 (1)y����x2��11(2)��ֹ��ֻͨ��ʱ��Ϊ32Сʱ��
�����������κ�����Ӧ�ã�����ϵ�����������ϵ�������뷽�̵Ĺ�ϵ��
��1�������������ص�������κ�������ʽ����B������뼴����⡣
��2��ˮ�浽����C�ľ��벻����5��ʱ����ˮ����ӵ�ED�ľ���h����Ϊ6����6�����������κ�����ϵʽ�����t��ֵ��������ɵõ���ֹ��ֻͨ�е�ʱ�䡣
(1)y����x2��11(2)��ֹ��ֻͨ��ʱ��Ϊ32Сʱ��
�����������κ�����Ӧ�ã�����ϵ�����������ϵ�������뷽�̵Ĺ�ϵ��
��1�������������ص�������κ�������ʽ����B������뼴����⡣
��2��ˮ�浽����C�ľ��벻����5��ʱ����ˮ����ӵ�ED�ľ���h����Ϊ6����6�����������κ�����ϵʽ�����t��ֵ��������ɵõ���ֹ��ֻͨ�е�ʱ�䡣 �����Ŀڴ���װ��2������2��������ɫ�������ͬ����
�¼�A���������һ�����Żأ����������һ�������ζ���������
�¼�B���������һ����Żأ����������һ�������ζ�������ͬ��ɫ����
�ԱȽ����������¼������Ŀ������ĸ�����˵�����ɣ�
 �¼�B�����Դ�
��������������������⿼��Կ����Դ�С������,ͨ���б������Զ��¼�A���¼�B�Ŀ����ԵĴ�С���бȽ�.
��������� �����¼�A�����ܵĽ�����±���ʾ��
��һ��
��1
��2
��1
��2
�ڶ���
��2
��1
��2
��1
��1
��2
��1
��2
��2
��1
��2
��1
...
�¼�B�����Դ�
��������������������⿼��Կ����Դ�С������,ͨ���б������Զ��¼�A���¼�B�Ŀ����ԵĴ�С���бȽ�.
��������� �����¼�A�����ܵĽ�����±���ʾ��
��һ��
��1
��2
��1
��2
�ڶ���
��2
��1
��2
��1
��1
��2
��1
��2
��2
��1
��2
��1
... ��ͼ�����ı���ABCD�У�AD��BC��BC��AD����B���C���࣬��AB��CD�ֱ�ƽ�Ƶ�EF��EG��λ�ã����EFGΪ________�����Ρ�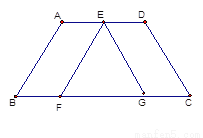
 ֱ��
����������AB��CD�ֱ�ƽ�Ƶ�EF��EG��λ�ú�B�Ķ�Ӧ���ǡ�EFG����C�Ķ�Ӧ���ǡ�EGF���֡ߡ�B���C���࣬���EFG���EGF���࣬
���ڡ�EFG�У���FEG=90�㣨�������ڽǺͶ����������EFGΪRt��EFG.
ֱ��
����������AB��CD�ֱ�ƽ�Ƶ�EF��EG��λ�ú�B�Ķ�Ӧ���ǡ�EFG����C�Ķ�Ӧ���ǡ�EGF���֡ߡ�B���C���࣬���EFG���EGF���࣬
���ڡ�EFG�У���FEG=90�㣨�������ڽǺͶ����������EFGΪRt��EFG.