题目内容
已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.
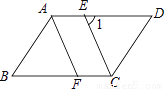
 (1)证明见解析;(2)50°.
【解析】试题分析:(1)由平行四边形的性质得出AB=CD,AD∥BC,∠B=∠D,得出∠1=∠DCE,证出∠AFB=∠1,由AAS证明△ABF≌△CDE即可;(2)由(1)得∠1=∠DCE=65°,由平行四边形的性质和三角形内角和定理即可得出结果.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AB=CD,AD∥BC,∠B=∠D, ∴∠1=∠DCE...
(1)证明见解析;(2)50°.
【解析】试题分析:(1)由平行四边形的性质得出AB=CD,AD∥BC,∠B=∠D,得出∠1=∠DCE,证出∠AFB=∠1,由AAS证明△ABF≌△CDE即可;(2)由(1)得∠1=∠DCE=65°,由平行四边形的性质和三角形内角和定理即可得出结果.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AB=CD,AD∥BC,∠B=∠D, ∴∠1=∠DCE...
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
图1中所示程序进行计算:(1)若输入-3,求y的值;(2)若第一次输入x,输出的结果记为y1,第二次输入(1-x),计算的结果记为y2,要使y1>y2,你怎样选择x的值,并把x值的范围在图2中的数轴上表示出来.

 (1)-8;(2)x>0.5.
【解析】【试题分析】(1)设输入的数为x,则输出的结果y=2(x-1),当x=-3时,y=-8;
(2)y1=2(x-1);y2=-2x,又根据y1>y2,得到2(x-1)>-2x,解不等式得x>0.5,画数轴见解析.
【试题解析】
(1)y=(x-1)·2=2(x-1),当x=-3时,y=2×(-3-1)=-8;
(2)由题意知y1=...
(1)-8;(2)x>0.5.
【解析】【试题分析】(1)设输入的数为x,则输出的结果y=2(x-1),当x=-3时,y=-8;
(2)y1=2(x-1);y2=-2x,又根据y1>y2,得到2(x-1)>-2x,解不等式得x>0.5,画数轴见解析.
【试题解析】
(1)y=(x-1)·2=2(x-1),当x=-3时,y=2×(-3-1)=-8;
(2)由题意知y1=... 解不等式,并把解集在数轴上表示出来:
(1)5x﹣6≤2(x+3);
(2)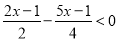
 (1)x≤4; (2)x>﹣1,
【解析】【试题分析】(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
【试题解析】(1)去括号,得:5x﹣6≤2x+6,
移项,得:5x﹣2x≤6+6,
合并同类项,得:3x≤12,
系数化为1,得:x≤4,
...
(1)x≤4; (2)x>﹣1,
【解析】【试题分析】(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
【试题解析】(1)去括号,得:5x﹣6≤2x+6,
移项,得:5x﹣2x≤6+6,
合并同类项,得:3x≤12,
系数化为1,得:x≤4,
... 如图,当y<0时,自变量x的范围是( )
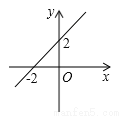
A.x<-2 B.x>-2 C.x<2 D.x>2
 A.
【解析】
试题解析:由图象可得,一次函数的图象与x轴的交点为(-2,0),当y<0时,x<-2.
故选A.
A.
【解析】
试题解析:由图象可得,一次函数的图象与x轴的交点为(-2,0),当y<0时,x<-2.
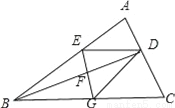
故选A. 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2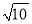 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
 (1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:...
(1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:... 如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是_______.
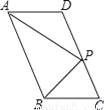
 24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD...
24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD... 如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
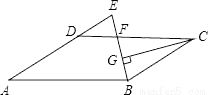
A. 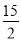 B.
B. 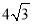 C.
C. 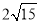 D.
D. 
 C
【解析】∵∠ABC的平分线交CD于点F,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,
∴DE=4,
∵DC∥AB,
∴,
∴,
∴EB=6,
∵CF=CB,CG⊥BF,
∴BG=BF=2...
C
【解析】∵∠ABC的平分线交CD于点F,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,
∴DE=4,
∵DC∥AB,
∴,
∴,
∴EB=6,
∵CF=CB,CG⊥BF,
∴BG=BF=2... 如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第n个图形中共有三角形的个数为__.
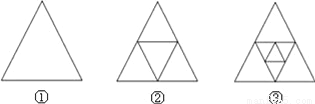
 4n﹣3
【解析】试题解析:第①是1个三角形,1=4×1-3;
第②是5个三角形,5=4×2-3;
第③是9个三角形,9=4×3-3;
∴第n个图形中共有三角形的个数是4n-3
4n﹣3
【解析】试题解析:第①是1个三角形,1=4×1-3;
第②是5个三角形,5=4×2-3;
第③是9个三角形,9=4×3-3;
∴第n个图形中共有三角形的个数是4n-3 下列说法错误的是( )
A. 对角线互相平分的四边形是平行四边形
B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边相等,另一组对边平行的四边形是平行四边形
 D
【解析】一组对边相等,另一组对边平行不能判定四边形为平行四边形,故D选项错误.
故选D.
D
【解析】一组对边相等,另一组对边平行不能判定四边形为平行四边形,故D选项错误.
故选D. 
