题目内容
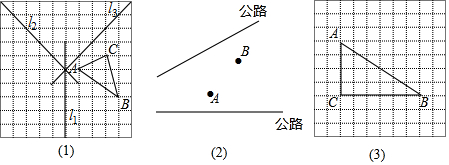
1.作图:(1)在如图1网格中画图:
①画△A1B1C1,使它与△ABC关于l1对称;
②画△A2B2C2,使它与△A1B1C1关于l2对称;
③画△A3B3C3,使它与△A2B2C2关于l3对称;
④画出△A3B3C3与△ABC的对称轴.
(2)“西气东输”是造福子孙后代的创世纪工程.现有两条高速公路和A、B两个城镇(如图2),准备建立一个燃气中心站P,使中心站到两条公路距离相等,并且到两个城镇距离相等,请你画出中心站位置.
(3)在图3网格中的线段AB上找一点P使得点P到AC、BC的距离相等;并在射线AP上找一点Q使得QA=QB(必须标注出格点).
分析 (1)根据轴对称性质分别作出各定点关于直线对称的对应点,连接即可得;
(2)到两条公路的距离相等,则要画两条公路的夹角的角平分线,到A,B两点的距离相等又要画线段AB的垂直平分线,两线的交点就是点P的位置;
(3)作∠ACB平分线,与AB交点即为所求点P,再作线段AB的中垂线,与射线AP交点即为点Q.
解答 解:(1)如图1,△A1B1C1、△A2B2C2、△A3B3C3、直线l即为所求;
(2)如图2所示,点P即为所求;
(3)如图2,点P、Q即为所求. .
.
点评 本题主要考查作图与应用设计作图,熟练掌握轴对称的性质、角平分线的性质、中垂线的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知关于x的二次函数y=a(x-1)2+a-3,当-2≤x≤3时,y>0,则a的取值范围( )
| A. | a>3 | B. | a<0或a>$\frac{3}{10}$ | C. | 0<a<$\frac{3}{10}$ | D. | $\frac{3}{10}$<a<3 |
13.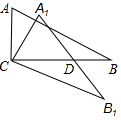 如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( )
如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( )
 如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( )
如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
10.把下列各式约分:
| (1)$\frac{{a}^{2}-ab}{a-b}$ | (2)$\frac{2{x}^{4}-4{x}^{3}}{x-2}$ | (3)$\frac{{x}^{2}-25}{{x}^{2}-5x}$ |
| (4)$\frac{-(2-x)}{-(y-2)(x-2)}$ | (5)$\frac{{x}^{2}+6x+9}{{x}^{2}-9}$ | (6)$\frac{{m}^{2}-8m+16}{{m}^{2}-4m}$ |
11.比较-$\frac{1}{3}$,-$\frac{1}{4}$,$\frac{1}{6}$的大小,结果正确的是( )
| A. | $\frac{1}{6}<-\frac{1}{4}<-\frac{1}{3}$ | B. | $\frac{1}{6}<-\frac{1}{3}<-\frac{1}{4}$ | C. | $-\frac{1}{4}<-\frac{1}{3}<\frac{1}{6}$ | D. | $-\frac{1}{3}<-\frac{1}{4}<\frac{1}{6}$ |
 已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根,k为正整数.
已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根,k为正整数.